Материальная точка. Система отсчета. Перемещение. Определение координаты
Решебник к сборнику задач по физике для 7- 9 классов, Перышкин А.В.
1404. Можно ли считать автомобиль материальной точкой при определении пути, который он проехал за 2 ч? за 2 с?
В первом случае можно. Во втором случае нельзя, потому что тело можно считать материальной точкой тогда, когда его размеры меньше расстояний, рассматриваемых в задаче.
1405. Можно ли рассматривать поезд длиной 200 м как материальную точку при определении времени, за которое он проехал расстояние 2 м?
Нельзя. Длина поезда больше пройденного им расстояния. Для рассмотрения поезда в качестве материальной точки расстояние, пройденное им, должно быть больше его собственной длины.
1406. Можно ли считать поезд длиной 200 м материальной точкой при определении времени, за которое он проехал мост длиной 800 м?
Можно.
1407. Муха ползет по краю блюдца из точки А в точку В (рис. 176). На рисунке покажите:
а) траекторию движения мухи;
б) перемещение мухи.
1408. При каком движении материальной точки путь, пройденный точкой, равен модулю перемещения?
При прямолинейном.
1409. Рота солдат прошла на север 4 км, затем солдаты повернули на восток и прошли еще 3 км. Найдите путь и перемещение солдат за все время движения. Нарисуйте в тетради траекторию их движения.
1410. Найдите координаты точек А, В и С в системе координат XOY (рис. 177). Определите расстояния между точками:
а) А и В, б) В и С, в) А и С.
1411. На рисунке 178 показаны перемещения трех материальных точек: s1, s2, s3. Найдите:
а) координаты начального положения каждой точки;
б) координаты конечного положения каждой точки;
в) проекции перемещения каждой точки на координатную ось OX;
г) проекции перемещения каждой точки на координатную ось OY;
д) модуль перемещения каждой точки.
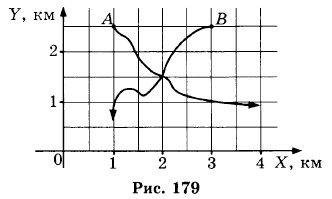
1413. Определите координаты пересечения траекторий двух муравьев А и В, которые движутся по траекториям, показанным на рисунке 179. При каком условии возможна встреча муравьев А и В?
1415. Мяч с расстояния h0 = 0,8 м от поверхности земли подбрасывают вертикально вверх на высоту h1 = 2,8 м от поверхности земли, затем мяч падает на землю. Нарисуйте координатную ось OX, направленную вертикально вверх с началом координат на поверхности земли. Покажите на рисунке:
а) координату x0 начального положения мяча;
б) координату xm максимального подъема мяча;
в) проекцию перемещения sx мяча за время полета.
1416. Решите предыдущую задачу, расположив начало координат в точке бросания мяча.
Материальная точка. Система отсчета. Перемещение. Определение координаты движущегося тела
1394. Определите координаты пересечения траекторий двух муравьев А и В, которые движутся по траекториям, показанным на рисунке 179. При каком условии возможна встреча муравьев А и В?
а) модуль перемещения автомобиля;
б) модуль перемещения велосипедиста;
в) проекцию перемещения каждого тела на ось ОХ;
г) путь, пройденный каждым телом;
д) расстояние между телами в начальный момент времени;
е) расстояние между телами в конечный момент времени.
1396. Мяч с расстояния h0 = 0,8 м от поверхности земли подбрасывают вертикально вверх на высоту h1 = 2,8 м от поверхности земли, затем мяч падает на землю. Нарисуйте координатную ось ОХ, направленную вертикально вверх с началом координат на поверхности земли. Покажите на рисунке:
а) координату х0 начального положения мяча;
б) координату хm максимального подъема мяча;
в) проекцию перемещения sx мяча за время полета.
1397. Решите предыдущую задачу, расположив начало координат в точке бросания мяча.
На рисунке 184 изображены автомобиль и велосипедист двигающиеся навстречу друг другу начальная
1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Типовая задача «Уравнение координаты (нахождение неизвестной величины)»
Задача № 1. В начальный момент времени тело находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.
Типовая задача «Уравнение координаты. Движение двух тел»
Задача № 2. Движение двух тел задано уравнениями x1 = 20 – 8t и х2 = –16 + 10t (время измеряется в секундах, координата — в метрах). Определите для каждого тела начальную координату, проекцию скорости, направление скорости. Вычислите время и место встречи тел.
Типовая задача «График координаты»
Задача № 3. Движение тела задано графиком координаты (зависимости координаты от времени). По графику определите: а) начальную координату тела; б) проекцию скорости тела; в) направление движения тела (по оси х или против оси х); г) запишите уравнение координаты.
Типовая задача «График координаты. Движение нескольких тел»
Задача № 4. На рисунке изображены графики движения трех тел. Изучив рисунок, для каждого тела определите: а) начальную координату; б) скорость; в) направление движения; г) запишите уравнение координаты.
ЗАДАЧИ ПОСЛОЖНЕЕ
Задача № 5. На рисунке представлены графики зависимости координаты х от времени t для пяти тел. Определите скорости этих тел. Проанализируйте точки пересечения графиков. Постройте графики зависимости скорости от времени.
РЕШЕНИЕ:
РЕШЕНИЕ:
Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение.
Задачи, описывающие движение, содержат два типа величин: векторные (имеющие направление) и скалярные (выражающиеся только числом). К векторным величинам при описании равномерного прямолинейного движения относятся скорость и перемещение.
Для перехода от векторов к скалярам выбирают координатную ось и находят проекции векторов на эту ось, руководствуясь следующим правилом: если вектор сонаправлен с осью, то его проекция положительна, если противоположно направлен — отрицательна. (Могут быть и более сложные случаи, когда вектор не параллелен координатной оси, а направлен к ней под некоторым углом.) Поэтому при решении задачи обязательно нужно сделать чертеж, на котором изобразить направления всех векторов и координатную ось. При записи «дано» следует учитывать знаки проекций.
При решении задач все величины должны выражаться в международной системе единиц (СИ), если нет специальных оговорок.
В решении задачи единицы величин не пишутся, а записываются только после найденного значения величины.
Это конспект по теме «ЗАДАЧИ на Прямолинейное равномерное движение с решениями». Выберите дальнейшие действия:
На рисунке 184 изображены автомобиль и велосипедист двигающиеся навстречу друг другу начальная
Нельзя, так как скорость движения воздушного шара равна скорости ветра.
В системе отсчета «Земля» точка колеса, соприкасающаяся с рельсом, имеет мгновенную скорость, равную нулю. В сторону, обратную движению вагона, перемещаются точки реборды, находящиеся ниже точки соприкосновения колеса и рельса.
Задача легко решается в системе координат, связанной с одной из машин. Пусть В неподвижна. Тогда машина А относительно В как бы участвует в двух движениях: со скоростью v1 относительно земли и со скоростью вместе с землей. Построив параллелограмм (рис. 286), найдем скорость v0 машины А относительно неподвижной машины В. Длина перпендикуляра ВС и выражает наименьшее расстояние, на которое сближаются машины.
Путь за какую-нибудь секунду любого движения численно равен средней скорости за эту секунду. Так как поезд движется с ускорением а>0, то скорость его все время возрастает. Если к концу четвертой секунды скорость равна 6 м/с, то в начале четвертой секунды она была меньше 6 м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6 м/с.
На рисунке 184 изображены автомобиль и велосипедист двигающиеся навстречу друг другу начальная
Решение:
Велосипедист проедет до встречи расстояние

Автомобиль проедет до встречи расстояние

Подставим выражение для х в формулу (2)
Расстояние до встречи, пройденное велосипедистом
Если скорости увеличатся в два раза, то время до встречи
Расстояние до встречи, пройденное велосипедистом
Т.е. место встречи не изменится.
Ответ: