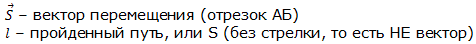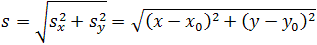на рисунке изображена траектория движения автомобиля определите модуль вектора перемещения

1.1. Кинематика

Примеры заданий ЕГЭ по теме 1.1. «Кинематика»

Часть 1

При выполнении заданий уровня А нужно поставить знак «х» в клеточку, номер которой соответствует номеру выбранного варианта ответа.

А1. На рисунке изображена траектория движения автомобиля. Модуль вектора перемещения из точки А в точку В составляет

1) 6 км 2) 10 км 3) 3,5 км 4) 5 км

А2. На рисунке а приведен график движения тела. Ему соответствует зависимость скорости от времени, представленная на

АЗ. Тело двигалось из точки А в точку В с переменной скоростью, преодолев первый участок пути в 5 м за 8 с, второй участок в 3 м — за 10 с и третий участок длиной 10 м за 18 с. Средняя путевая скорость движения между точками А и В составила

1) 0,5 м/с 2) 2 м/с 3) 0,3 м/с 4) 1 м/с

А4. График зависимости скорости от времени, изображенный на рисунке, описывает:

1) равномерное движение 3) равнозамедленное движение

2) равноускоренное движение 4) отсутствие какого-либо движения

А5. Точка совершает равномерное движение вдоль окружности радиусом В = 5 м со скоростью 3 м/с. Ее центростремительное ускорение при этом равно:

1) 2,5 м/с2 2) 1,8 м/с2 3) 1,5 м/с2 4) 3 м/с2.

А6. Угловая скорость минутной стрелки часов составляет:

1) 0,00174 рад/с 2) 0,005 рад/с 3) 0,003 рад/с 4) 0,04 рад/с.

А7. В безветренную погоду капли дождя падают на землю вертикально. При этом след от капель на окне поезда, движущегося с постоянной скоростью относительно наблюдателя, стоящего на платформе, представляет собой:

1) прямую горизонтальную линию 3) гиперболу

2) прямую вертикальную линию 4) параболу.

Часть 2

Ответом к заданиям В1— В2 будет некоторое число. Это число нужно записать без указания единиц измерения физических величин.

В1. Пользуясь графиком зависимости скорости от времени, изображенным на рисунке, определите путь, пройденный телом за первые 3 минуты.

В2. Мгновенное ускорение тела, движущегося по окружности, равно 5 м/с2, при этом его центростремительное ускорение составляет 4 м/с2. Каково тангенциальное ускорение тела?

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

Источник

Содержание

Траектория

Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.

Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.

Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.

Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.

Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.

Вектор перемещения

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.

Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.

Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).

Рис. 1.1. Вектор перемещения и пройденный путь.

Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.

Правило сложения векторов

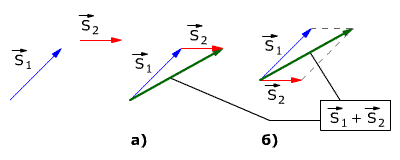
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).

Рис. 1.2. Сложение векторов перемещений.

На рис 1.2 показаны правила сложения векторов S1 и S2:

а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма

Проекции вектора перемещения

При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения 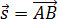(рис. 1.3).

Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно А_x и В_x. Длина отрезка А_xВ_x на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть

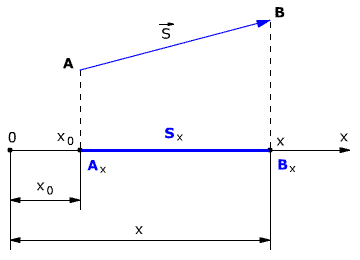
Рис. 1.3. Проекция вектора перемещения.

Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:

Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).

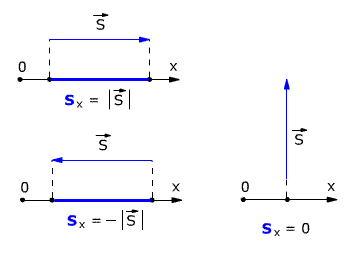
Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).

Рис. 1.4. Модули проекции вектора перемещения.

Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.

Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х₀ и у₀, то есть А(х₀, у₀). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.

Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).

Рис. 1.5. Движение тела на плоскости.

Определим проекции вектора перемещения на осях ОХ и OY:

На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как

По теореме Пифагора

Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:

Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.

Источник

На рисунке изображена траектория движения автомобиля определите модуль вектора перемещения

3.1 Как найти путь или перемещение по известной траектории движения?

В задачах при нахождении пути и перемещении необходимо помнить определения (1.6) и (1.7), то есть:

– для нахождения пути из геометрических соображений находим длину траектории;

– для нахождения перемещения, соединяем начальную точку с конечной и ищем длину получившегося вектора.

3.1.2 Тело прошло четверть окружности.

(1.26)

(1.27)

3.1.3 Тело прошло пол окружности.

(1.28)

(1.29)

3.14 Тело прошло три четверти окружности.

(1.30)

(1.31)

3.1.5 Тело прошло всю окружность.

(1.32)

(1.33)

Заметим, несмотря на то, что тело прошло какой-то путь, перемещение равно нулю, так как тело вернулось в исходную точку.

3.1.6 Тело повернулось по окружности на уголь α.

(1.34)

Перемещение найдем по теореме косинусов:

(1.35)

3.2 Тело движется «туда и обратно».

Тело движется в одном направлении n км, затем по этой же прямой возвращается обратно и проходит m км.

Нужно помнить, что путь — это длина всей траектории, то есть, для нахождения всего пути направление движения не учитываем, а просто суммируем:

(1.36)

Перемещение — это расстояние между начальной и конечной точкой:

(1.37)

3.3 Тело движется на север n км, затем поворачивает на восток (запад) и движется еще m км.

(1.38)

Перемещение найдем по теореме косинусов:

(1.39)

3.4. Как найти проекции и модуль перемещения на координатной плоскости?

При нахождении проекций нужно помнить, что перемещение — это вектор. Следовательно, все операции с перемещением производим как для обыкновенного вектора:

1) если известна длина вектора и его направление, то для нахождения проекций необходимо воспользоваться правилом в пункте 1.3.

2) если известны координаты конца и начала вектора перемещения, то необходимо воспользоваться правилом в пункте 1.4, а для нахождения модуля перемещения пунктом 1.5.

2.1 Равномерное прямолинейное движение.

2.1.1 Равномерное прямолинейное движение — это движение, при котором тело за любые равные промежутки времени совершает равные перемещения, двигаясь по прямой линии.

2.1.2 Скорость — векторная физическая величина, показывающая какое перемещение совершило тело за единицу времени:

(2.1)

При равномерном движении по прямой:

(2.2)

где S — путь, проходимый телом за время t.

Для учета направления движения эту формулу запишем в проекциях:

(2.3)

где — перемещение вдоль оси Ox за время t. Знак проекции зависит от направления скорости и оси координат (см. рис. 1):

2.1.3 График проекции скорости от времени.

Так скорость при равномерном движении по прямой является постоянной, то график будет представлять собой прямые линии, параллельные оси времени (см. рис. 2):

Направление движения: если график лежит над осью времени (1 и 2), то проекция положительна и тело движется по направлению оси Ox; в противном случае, когда график расположен ниже оси времени (3 и 4), то проекция скорости отрицательна и тело движется против оси Ox.

Значение скорости: чем дальше от оси времени лежит прямая, тем больше модуль скорости

2.1.4 Геометрический смысл площади под графиком в осях .

Для любого вида движения пройденный телом путь можно определить как площадь под графиком, когда на оси Oy отложена скорость, а на оси Ox — время. Это легко видеть непосредственно из рисунка для равномерного движения (см. рис. 3):

2.1.5 График проекции перемещения.

Из определения (2.3) проекция перемещения при равномерном прямолинейном движении определяется формулой:

(2.4)

График проекции перемещения при равномерном прямолинейном движении — это прямая, выходящая из начала координат.

Направление движения: если прямая лежит над осью времени (поднимается вверх), то тело движется в положительном направлении оси Ox (прямые 1 и 2); если прямая лежит под осью времени (опускается вниз), то тело движется против оси Ox.

Значение скорости: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль скорости

2.1.6 Закон движения.

Из определения (2.3) имеем:

(2.5)

где — начальная координата тела по оси Ox, x — координата тела в момент времени t, — проекция скорости на ось Ox.

При движении по прямой всегда возможно выбрать ось Ox вдоль этой прямой. Однако в некоторых случаях удобно рассматривать движение и вдоль оси Oy:

(2.6)

2.1.7 График изменения координаты.

Уравнение координаты при равномерном движении имеет вид (2.5).

График изменения координаты при равномерном движении — это прямая линия.

Направление движения: если с течением времени координата увеличивается (прямая поднимается вверх), то тело движется по направлению оси Ox (прямые 1 и 2); если координата уменьшается (прямая опускается вниз), то движение происходит против оси Ox.

Значение скорости: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль скорости; где — изменение координаты за время

Начальная координата тел — точка пересечения прямой с вертикальной осью (на рисунке это ось Ox, но мы привыкли, что вертикальная ось — ось Ox).

Время и место встречи двух тел — точка пересечения графиков координат двух тел; из точки пересечения следует опустить перпендикуляры на ось времени и ось координат.

Пересечение прямой с осью времени — точка пересечения прямой с ось времени означает, что тело проехало мимо начала отсчета.

2.2 Средняя скорость неравномерного движения.

2.2.1 Неравномерное движение — это движение с переменной скоростью. Скорость со временем может меняться как угодно — по любому закону.

2.2.2 Средняя векторная скорость.

(2.7)

где — перемещение за время t.

2.2.3 Средняя путевая (скалярная) скорость.

(2.8)

где L — весь путь, пройденный за время t.

2.3 Относительность механического движения.

В определении системы отсчета было сказано, что за тело отсчета можно выбирать абсолютно любое тело. В зависимости от выбора такого тела, то есть от выбора системы отсчета, одно и то же движение будет выглядеть по-разному. Например, сидим в движущейся машине — относительно машины мы неподвижны, относительно земли — движемся. Покой относителен. Движение тела относительно и положение тела относительно.

2.3.1 Правило сложения перемещений.

Векторная сумма перемещений

(2.9)

где — перемещение относительно неподвижной системы отсчета (НСО), — перемещение относительно подвижной системы отсчета (ПСО), — перемещение самой подвижной системы отсчета (СПСО).

2.3.2 Правило сложения скоростей.

Векторная сумма скоростей

(2.10)

где — скорость относительно неподвижной системы отсчета (НСО), — скорость относительно подвижной системы отсчета (ПСО), — перемещение самой подвижной системы отсчета (СПСО).

2.3.3 Относительная скорость.

Векторная разность скоростей

(2.11)

где — скорость первого тела относительно второго (относительная скорость), — скорость первого тела, — скорость второго тела.

2.2.1 Как перевести из км/ч в м/с и т. д?

В задачах часто необходимо переводить из одних единиц измерения в другие:

1 км/ч = (1000 м)/(3600 с) = 5/18 м/с, (2.12)

1 км/с = 1000 м/с, (2.14)

1 м/мин = 1/60 м/с. (2.16)

Например, если то для того, чтобы перевести в м/с, нужно умножить на 5/18:

2.2.2 Как найти скорость тела, если известен закон движения?

Закон равномерного движения имеет вид (2.5):

Видим, что в этой формуле скорость стоит коэффициентом перед временем. Поэтому, если в условии задачи дан закон движения, необходимо посмотреть на коэффициент перед t — это и есть скорость.

Например, пусть закон движения имеет вид: В данном случае коэффициент перед t равен 5, следовательно,

2.2.3 Как определить скорость по графику координаты от времени?

Закон равномерного движения имеет вид (2.5):

Графиком этого закона является прямая линия. Так как — коэффициент перед t, то является угловым коэффициентом прямой.

(2.17)

То, что график 1 «поднимается вверх», означает — тело едет в положительном направлении оси Ox.

(2.18)

То, что график 2 «опускается вниз», означает — тело едет в отрицательном направлении оси Ox.

Для определения и выбираем такие точки на графике, в которых можно точно определить значения, как правило, это точки, находящиеся в вершинах клеток.

2.2.4 Как найти закон движения, если известны координаты тела в моменты времени и ?

Пусть в момент времени тело находилось в точке с координатой а в момент времени тело находилось в точке с координатой Закон равномерного движения имеет вид (2.5).

Для времени имеем:

(2.19)

Для времени имеем:

(2.20)

Решая систему уравнений (2.19) и (2.20), получим

(2.21)

(2.22)

2.2.5 Как найти графически момент и координату встречи двух тел?

Пусть даны законы движения двух тел: и Согласно пункту 2.5 графиками обоих законов являются прямые линии. Необходимо на одном графике построить оба закона.

Графики пересекаются в одной точке. Координаты этой точки и являются временем и местом встречи.

2.2.6 Как аналитически найти координату и время встречи двух тел?

Пусть даны законы движения двух тел: и В момент встречи тела оказываются в одной координате, то есть и необходимо решить уравнение:

(2.17)

Решение уравнения имеет вид:

(2.18)

Для нахождения координаты достаточно подставить вместо t найденное значение в любой из законов движения:

2.2.7 Как найти среднюю скорость, если тело половину пути проехало со скоростью а вторую половину пути

В нашем случае, так как на каждой половине пути тело едет с постоянной скоростью, то

(2.19)

(2.20)

В общем случае, если весь путь разбить на n равных участков, на каждом из которых тело едет с постоянной скоростью, то

(2.21)

Формула (2.21) справедлива только если весь путь разбит на равные участки. Если же разбиение будет иное, то, естественно, формула для нахождения средней скорости, будет иной.

2.2.8 Как найти среднюю скорость, если тело половину времени проехало со скоростью а вторую половину времени

В нашем случае, так как каждую половину времени тело едет с постоянной скоростью, то

(2.22)

(2.23)

В общем случае, если все время разбито на n равных промежутков, на каждом из которых тело едет с постоянной скоростью, то

(2.24)

Формула (2.24) справедлива только если все время разбито на равные промежутки. Если же разбиение будет иное, то, естественно, формула для нахождения средней скорости, будет иной.

2.2.9 Как найти скорость, с которой движется моторная лодка по течению реки?

Согласно формуле (2.10) скорость тела относительно неподвижной системы отсчета (в нашем случае земли), равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета (в нашем случае — собственная скорость лодки).

При движении по течению вектора и направлены в одну сторону, следовательно, получаем сложение двух векторов, направленных в одну сторону — используем формулу (1.15):

(2.25)

Таким образом, при движении любого тела по течению его скорость определяется формулой (2.25).

2.2.10 Как найти скорость, с которой движется моторная лодка против течения реки?

Согласно формуле (2.10) скорость тела относительно неподвижной системы отсчета (в нашем случае земли) равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета (в нашем случае — собственная скорость лодки).

Перепишем формулу в виде:

Вектора и направлены в одну сторону, следовательно, получаем вычитание двух векторов, направленных в одну сторону — используем формулу (1.16):

(2.26)

2.2.11 Как найти скорость, с которой движется моторная лодка, если ее скорость направлена перпендикулярно течению реки?

В данном случае вектора и направлены перпендикулярно, следовательно, получаем задачу о сложении взаимно перпендикулярных векторов — используем формулу (1.17):

(2.27)

2.2.12 Как найти расстояние, на которое снесет лодку, если ее скорость направлена перпендикулярно скорости реки?

В результате сложения скоростей по формуле (2.10) скорость тела, относительно земли равна и направлена по прямой OD. В результате, когда тело окажется на противоположном берегу, оно попадет в точке D, и его снесет на длину

Треугольник OAB подобен треугольнику OCD:

(2.28)

2.2.13 Как найти скорость, с которой движется моторная лодка, если ее скорость направлена под углом φ к скорости течения реки?

В результате сложения скоростей по формуле (2.10) скорость тела относительно земли равна и направлена по прямой OB. Как видим, получили треугольник, в котором известен один из углов — Тогда по теореме косинусов:

(2.29)

2.2.14 Как найти расстояние, на которое снесет лодку, если ее скорость направлена под углом к скорости течения реки?

В результате сложения скоростей по формуле (2.10) скорость тела относительно земли равна и направлена по прямой OB. В результате, когда тело окажется на противоположном берегу, оно попадет в точке В, и его снесет на длину

В задачах, когда движение происходит в плоскости, то есть и вдоль оси Ox, и вдоль оси Oy (см. рис. 12), необходимо введение системы координат для того, чтобы упростить рассмотрение задачи.

Проекция

(2.30)

Проекция

(2.31)

Формулы (2.30) и (2.31) не просто результат математической операции нахождения проекции, и имеют физический смысл: со скоростью тело плывет вдоль оси Ox, то есть по течению; со скоростью тело переплывает реку. Например, время, за которое тело переплывет реку, можно найти просто поделив ширину реки на

(2.32)

(2.33)

2.2.15 Под каким углом α нужно направить собственную скорость лодки, чтобы за минимальное время переплыть реку?

Согласно формуле (2.31) скорость, с которой лодка переплывает реку, равна:

Очевидно, что время будет минимальным, если будет максимальным, то есть

2.2.16 С какой скоростью машина обгоняет вторую машину, если они движутся в одну сторону?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина также движется вправо со скоростью Скорость обгона — это скорость, с которой 1-ая машина движется относительно 2-ой, то есть — это относительная скорость, и она определяется формулой (1.16):

Так как и направлены в одну сторону, то получили задачу о вычитании векторов, направленных в одну сторону — формула (1.16):

(2.34)

Заметим, что при обгоне, естественно поэтому

2.2.17 За какое время проедут мимо друг друга два поезда, двигающиеся в одном направлении?

Пусть длина 1-го поезда а скорость 2-го поезда Скорость обгона определяется формулой (2.34). Тогда

(2.35)

2.2.18 С какой скоростью машина едет навстречу вторую машину, если они движутся в противоположных направлениях?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина движется влево со скоростью Скорость движения навстречу — это скорость, с которой 1-ая машина движется относительно 2-ой, то есть — это относительная скорость, и она определяется формулой (1.16):

Перепишем эту формулу в виде:

(2.36)

2.2.19 За какое время проедут мимо друг друга два поезда, двигающиеся в противоположных направлениях?

Пусть длина 1-го поезда а скорость 2-го поезда Скорость обгона определяется формулой (2.34). Тогда

(2.37)

2.2.20 Как найти относительную скорость, если тела движутся по взаимно перпендикулярным направлениям?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина движется перпендикулярно первой со скоростью Относительная скорость определяется формулой (1.16):

Так как вектора и перпендикулярны, то воспользуемся формулой (1.18):

(2.38)

3.1. Равнопеременное движение по прямой.

3.1.1. Равнопеременное движение по прямой — движение по прямой с постоянным по модулю и направлению ускорением:

3.1.2. Ускорение () — физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.

(3.1)

где — начальная скорость тела, — скорость тела в момент времени t.

В проекции на ось Ox:

(3.2)

где — проекция начальной скорости на ось Ox, — проекция скорости тела на ось Ox в момент времени t.

Знаки проекций зависят от направления векторов и оси Ox.

(3.3)

(3.4)

3.1.3. График проекции ускорения от времени.

При равнопеременном движении ускорение постоянно, поэтому будет представлять собой прямые линии, параллельные оси времени (см. рис. 3.3):

Значение ускорения: чем дальше от оси времени лежит прямая, тем больше модуль ускорения

3.1.4. Скорость при равнопеременном движении.

(3.5)

В проекции на ось Ox:

(3.6)

Для равноускоренного движения:

(3.7)

Для равнозамедленного движения:

(3.8)

3.1.5. График проекции скорости в зависимости от времени.

График проекции скорости от времени — прямая линия.

Направление движения: если график (или часть его) находятся над осью времени, то тело движется в положительном направлении оси Ox.

Значение ускорения: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль ускорения; где — изменение скорости за время

Пересечение с осью времени: если график пересекает ось времени, то до точки пересечения тело тормозило (равнозамедленное движение), а после точки пересечения начало разгоняться в противоположную сторону (равноускоренное движение).

3.1.6. Геометрический смысл площади под графиком в осях

Площадь под графиком, когда на оси Oy отложена скорость, а на оси Ox — время — это путь, пройденный телом.

На рис. 3.5 нарисован случай равноускоренного движения. Путь в данном случае будет равен площади трапеции:

(3.9)

3.1.7. Формулы для расчета пути

(3.10)

(3.12)

(3.11)

(3.13)

(3.14)

Все формулы, представленные в таблице, работают только при сохранении направления движения, то есть до пересечения прямой с осью времени на графике зависимости проекции скорости от времени.

Если же пересечение произошло, то движение проще разбить на два этапа:

до пересечения (торможение):

(3.15)

(3.16)

После пересечения (разгон, движение в обратную сторону)

(3.17)

(3.18)

(3.19)

(3.20)

В формулах (3.17)—(3.20) — время от начала движения до пересечения с осью времени (время до остановки), — путь, который прошло тело от начала движения до пересечения с осью времени, — время, прошедшее с момента пересечения оси времени до данного момента t, — путь, который прошло тело в обратном направлении за время, прошедшее с момента пересечения оси времени до данного момента t, — модуль вектора перемещения за все время движения, L — путь, пройденный телом за все время движения.

За время тело пройдет путь:

(3.21)

За время тело пройдет путь:

(3.22)

(3.23)

За промежуток можно принимать любой отрезок времени. Чаще всего с.

Если то

(3.24)

Тогда за 1-ую секунду тело проходит путь:

Если внимательно посмотрим, то увидим, что и т. д.

Таким образом, приходим к формуле:

(3.25)

Словами: пути, проходимые телом за последовательные промежутки времени соотносятся между собой как ряд нечетных чисел, и это не зависит от того, с каким ускорени1111

Скорость тела увеличилась в n раз:

Скорость уменьшилась в n раз:

Скорость увеличилась на 2 м/с:

Во сколько раз увеличилась скорость?

Во сколько раз уменьшилась скорость?

Как изменилась скорость?

На сколько увеличилась скорость?

На сколько уменьшилась скорость?

Тело достигло наибольшей высоты:

Тело прошло половину расстояния:

Тело бросают с земли: (последнее условие часто ускользает из вида — если у тела скорость равна нулю, например у ручки, лежащей на столе, оно может полететь само вверх?), начальная скорость направлена вверх.

Тело бросают вниз: начальная скорость направлена вниз.

Тело бросают вверх: начальная скорость направлена вверх.

В момент падения на землю:

Тело выпадает из аэростата (воздушного шара): начальная скорость равна скорости аэростата (воздушного шара) и направлена в ту же самую сторону.

3.2.2. Как по графику скорости определить ускорение?

Закон изменения скорости имеет вид (3.6):

Графиком этого уравнения является прямая линия. Так как — коэффициент перед t, то является угловым коэффициентом прямой.

(3.50)

То, что график 1 «поднимается вверх», означает — проекция ускорения положительна, т. е. вектор направлен в положительном направлении оси Ox. Пересечение графика с осью — изменение направления движения на противоположное.

(3.51)

То, что график 2 «опускается вниз», означает — проекция ускорения отрицательна, т. е. вектор направлен в отрицательном направлении оси Ox. Пересечение графика с осью — изменение направления движения на противоположное.

3.2.3. Как по графику скорости определить пройденный путь и перемещение?

Как сказано в пункте 3.1.6 путь можно как площадь под графиком зависимости скорости от ускорения. Простой случай показан в пункте 3.1.6. Рассмотрим более сложный вариант, когда график скорости пересекает ось времени.

Напомним, что путь может только увеличиваться, поэтому путь, который проехало тело в примере на рисунке 9 равен:

(3.52)

где и — площади фигур, закрашенных на рисунке.

Для определения перемещения нужно заметить, что в точках и тело меняет направление движения. Проезжая путь тело движется в положительном направлении оси Ox, так как график лежит над осью времени. Проезжая путь тело движется в обратную сторону, в отрицательном направлении оси Ox так как график лежит под осью времени. Проезжая путь тело движется в положительном направлении оси Ox, так как график лежит над осью времени. Таким образом, перемещение равно:

(3.53)

Еще раз обратим внимание:

1) пересечение с осью времени означает поворот в обратную сторону;

2) площадь графика, лежащего под осью времени положительна и входит со знаком «+» в определение пройденного пути, но со знаком «−» в определении перемещения.

3.2.4. Как из графика зависимости ускорения от времени определить зависимость скорости от времени и координаты от времени?

Для того, чтобы определить требуемые зависимости необходимы начальные условия — значения скорости и координаты в момент времени Без начальных условий решить однозначно данную задачу невозможно, поэтому, как правило, в условии задачи они даны.

В данном примере постараемся привести все рассуждения в буквах, для того, чтобы частном примере (при подстановке цифр) не потерять суть действий.

Пусть в момент времени скорость тела равна нулю и начальная координата

1) От 0 до

Начальные значения скорости и координаты определяем из начальных условий, а ускорение из графика:

следовательно, движение равноускоренное и закон изменения скорости имеет вид:

(3.54)

(3.55)

К концу данного промежутка времени () скорость () и координата () будут равны (вместо времени в формулы (3.54) и (3.55) нужно подставить ):

(3.56)

(3.57)

2) От до

Начальное значение скорости на этом промежутке должно быть равно конечному значению на предыдущем промежутке, начальное значение координаты равно конечному значению координаты на предыдущем промежутке, а ускорение определяем из графика:

следовательно, движение равноускоренное и закон изменения скорости имеет вид:

(3.58)

(3.59)

К концу данного промежутка времени () скорость () и координата () будут равны (вместо времени в формулы (3.58) и (3.59) нужно подставить ):

(3.60)

(3.61)

3) От до

(3.62)

следовательно, движение равноускоренное и закон изменения скорости имеет вид:

(3.63)

(3.64)

К концу данного промежутка времени () скорость () и координата () будут равны (вместо времени в формулы (3.63) и (3.64) нужно подставить ):

(3.65)

(3.66)

Для лучшего понимания построим полученные результаты на графике (см. рис. 11)

На графике скорости:

1) От 0 до прямая линия, «поднимающаяся вверх» (т. к. );

2) От до горизонтальная прямая линия (т. к. );

3) От до : прямая линия, «опускающаяся вниз» (т. к. ).

На графике координаты:

1) От 0 до : парабола, ветви которой направлены вверх (т. к. );

2) От до : прямая линия, поднимающаяся вверх (т. к. );

3) От до : парабола, ветви которой направлены вниз (т. к. ).

3.2.5. Как из графика закона движения записать аналитическую формулу закона движения?

Пусть дан график равнопеременного движения.

Закон равнопеременного движения имеет вид (3.26):

В этой формуле три неизвестные величины: и

Для определения достаточно посмотреть на значение функции при Для определения двух других неизвестных выбираем две точки на графике, значения которых мы можем точно определить — вершины клеток. Получим систему:

(3.67)

При этом считаем, что нам уже известно. Умножим 1-ое уравнение системы на а 2-ое уравнение на :

(3.68)

Вычтем из 1-го уравнения 2-ое, после чего получаем:

(3.69)

Полученное из данного выражения значение подставим в любое из уравнений системы (3.67) и решим полученное уравнение относительно :

(3.70)

3.2.6. Как по известному закону движения определить закон изменения скорости?

Закон равнопеременного движения имеет вид (3.26):

Это его стандартный вид для данного типа движения и никак иначе он выглядеть не может, поэтому его стоит запомнить.

В данном законе коэффициент перед t — это значение начальной скорости, коэффициент пред — это ускорение, деленное пополам.

Например, пусть дан закон:

И уравнение скорости имеет вид:

Таким образом, для решения подобных задач, необходимо точно помнить вид закона равнопеременного движения (3.26) и смысл коэффициентов, входящих в это уравнение.

Однако, можно пойти и иным путем. Вспомним формулу (3.42):

(3.71)

3.2.7. Как определить место и время встречи?

Пусть даны законы движения двух тел:

В момент встречи тела оказываются в одной координате, то есть и необходимо решить уравнение:

(3.72)

Перепишем его в виде:

(3.73)

Это квадратное уравнение, общее решение которого приводить не будем, в силу его громоздкости. Квадратное уравнение либо не имеет решений, что означает — тела не встретились; либо имеет одно решение — одна единственная встреча; либо имеет два решения — две встречи тел.

Полученные решения необходимо проверять на физическую реализуемость. Самое главное условие: и то есть время встречи должно быть положительным.

Для решения этой задачи необходимо воспользоваться формулой (3.25):

Обозначим Тогда

(3.74)

(3.75)

Поделим уравнение (3.74) на (3.75) и получим:

(3.76)

3.2.9. Как движется тело, брошенное вверх с высоты h?

Тело, брошено вверх с высоты h со скоростью

Уравнение координаты y в произвольный момент времени:

(3.77)

Уравнение проекции скорости в произвольный момент времени:

(3.78)

Время подъема до наивысшей точки полета определяется из условия :

(3.79)

Для нахождения максимальной высоты H необходимо в (3.77) необходимо подставить :

(3.80)

Время всего полета определяется из условия Получаем уравнение:

(3.81)

Это квадратное уравнение, которое имеет два решения, но в данной задаче тело может оказаться в координате только один раз. Поэтому среди полученных решений нужно одно «убрать». Главный критерий отсева — время полета не может быть отрицательным:

(3.82)

Скорость в момент падения:

(3.83)

3.2.10. Как движется тело, брошенное вниз с высоты h?

Тело, брошено вверх с высоты h со скоростью

Уравнение координаты y в произвольный момент времени:

(3.84)

Уравнение проекции скорости в произвольный момент времени:

(3.85)

Время всего полета определяется из уравнения:

(3.86)

(3.87)

Скорость в момент падения:

(3.88)

3.2.11. Как движется тело брошенное вверх с поверхности земли?

Тело брошено вверх с поверхности земли со скоростью

Уравнение координаты y в произвольный момент времени:

(3.89)

Уравнение проекции скорости в произвольный момент времени:

(3.90)

Время подъема до наивысшей точки полета определяется из условия

(3.91)

Для нахождения максимальной высоты H необходимо в (3.89) необходимо подставить

(3.92)

Время всего полета определяется из условия Получаем уравнение:

(3.93)

Скорость в момент падения:

(3.94)

Заметьте, что что означает — время подъема равно времени падения на ту же высоту.

Также получили: то есть — с какой скоростью бросили, с такой же скоростью тело упало. Знак «−» в формуле (3.94) указывает, что скорость в момент падения направлена вниз, то есть против оси Oy.

3.2.12. Тело побывало на одной высоте дважды…

При бросании тела оно может дважды оказаться на одной высоте — первый раз при движении вверх, второй — при падении вниз.

1) Когда тело оказывается на высоте h?

Для тела, брошенного вверх с поверхности земли справедлив закон движения (3.89):

Когда тело окажется на высоте h его координата будет равна Получаем уравнение:

(3.95)

решение которого имеет вид:

(3.96)

(3.97)

2) Известны времена и когда тело оказалось на высоте h. Когда тело окажется на максимальной высоте?

Время полета с высоты h назад до высоты h равно Как уже было показано, время подъема равно времени падения до той же высоты, поэтому время полета от высоты h до максимальной высоты равно:

(3.98)

Тогда время полета от начала движения до максимальной высоты:

(3.99)

3) Известны времена и когда тело оказалось на высоте h. Чему равно время полета тела?

Все время полета равно:

(3.100)

4) Известны времена и когда тело оказалось на высоте h. Чему равна максимальная высота подъема?

(3.101)

3.2.13. Как движется тело, брошенное горизонтально с высоты h?

Тело, брошено горизонтально с высоты h со скоростью

Проекции начальной скорости на оси:

(3.102)

(3.103)

Проекции скорости в произвольный момент времени t:

(3.104)

Модуль скорости в произвольный момент времени t:

(3.105)

Координаты тела в произвольный момент времени t:

(3.106)

Время полета определяется из условия

(3.107)

Для определения дальности полета необходимо в уравнение для координаты x вместо t подставить

(3.108)

Для определения скорости тела в момент падения необходимо в уравнение (3.98) вместо t подставить

(3.109)

Угол, под которым падает тело на землю:

(3.110)

3.2.14. Как движется тело, брошенное под углом α к горизонту с высоты h?

Тело, брошено под углом α к горизонту с высоты h со скоростью

Проекции начальной скорости на оси:

(3.111)

(3.112)

Проекции скорости в произвольный момент времени t:

(3.113)

Модуль скорости в произвольный момент времени t:

(3.114)

Координаты тела в произвольный момент времени t:

(3.115)

Время полета до наивысшей точки определяется из условия

(3.116)

Скорость в наивысшей точке полета

(3.117)

Максимальная высота H определяется при подстановке в закон изменения координаты y времени

(3.118)

Все время полета находится из условия получаем уравнение:

(3.119)

(3.120)

Если подставим в закон изменения координаты x время то получим дальность полета L:

(3.121)

Скорость в момент падения

(3.122)

Угол, который образует вектор скорости с горизонталью в произвольный момент времени:

(3.123)

(3.124)

3.2.15. Как движется тело, брошенное под углом α к горизонту земли?

Тело, брошено под углом α к горизонту с поверхности земли со скоростью

Проекции начальной скорости на оси:

(3.125)

(3.126)

Проекции скорости в произвольный момент времени t:

(3.127)

Модуль скорости в произвольный момент времени t:

(3.128)

Координаты тела в произвольный момент времени t:

(3.129)

Время полета до наивысшей точки определяется из условия

(3.130)

Скорость в наивысшей точке полета

(3.131)

Максимальная высота H определяется при подстановке в закон изменения координаты y времени

(3.132)

Все время полета находится из условия получаем уравнение:

(3.133)

(3.134)

Снова получили, что то есть еще раз показали, что время подъема равно времени падения.

Если подставим в закон изменения координаты x время то получим дальность полета L:

(3.135)

Скорость в момент падения

(3.136)

Угол, который образует вектор скорости с горизонталью в произвольный момент времени:

(3.137)

(3.138)

то есть

3.2.16. Что такое настильная и навесная траектории?

Решим следующую задачу: под каким углом нужно бросить тело с поверхности земли, чтобы тело упало на расстоянии L от точки броска?

Дальность полета определяется формулой (3.135):

(3.139)

(3.140)

Из физических соображений ясно, что угол α не может быть больше 90°, поэтому, из серии решений уравнения (3.140) подходят два корня:

(3.141)

(3.142)

Траектория движения, для которой называется настильной траекторией. Траектория движения, для которой называется навесной траекторией.

3.2.17. Как пользоваться треугольником скоростей?

Как было сказано в 3.6.1 треугольник скоростей в каждой задаче будет иметь свой вид. Рассмотрим на конкретном примере.

Тело бросили с вершины башни со скорость так, что дальность полета максимальна. К моменту падения на землю скорость тела равна Сколько длился полет?

Построим треугольник скоростей (см. рис. 18). Проведем в ней высоту, которая, очевидно, равна Тогда площадь треугольника скоростей равна:

(3.143)

Здесь мы воспользовались формулой (3.121).

Найдем площадь этого же треугольника по другой формуле:

(3.144)

Так как это площади одного и того же треугольника, то приравняем формулы (3.143) и (3.144):

(3.145)

Как видно из формул для конечной скорости, полученных в предыдущих пунктах, конечная скорость не зависит от угла, под которым бросили тело, а зависит только значения начальной скорости и начальной высоты. Поэтому дальность полета по формуле (3.145) зависит только от угла между начальной и конечной скоростью β. Тогда дальность полета L будет максимальной, если примет максимально возможное значение, то есть

Таким образом, если дальность полета максимальна, то треугольник скоростей будет прямоугольным, следовательно, выполняется теорема Пифагора:

(3.146)

(3.147)

Свойством треугольника скоростей, который только что был доказан, можно пользоваться при решении других задач: треугольник скоростей является прямоугольным в задаче на максимальную дальность полета.

3.2.18. Как пользоваться треугольником перемещений?

Как было сказано в 3.6.2 треугольник перемещений в каждой задаче будет иметь свой вид. Рассмотрим на конкретном примере.

Тело бросают под углом β к поверхности горы, имеющей угол наклона α. С какой скоростью нужно бросить тело, чтобы оно упало ровно на расстоянии L от точки бросания?

Построим треугольник перемещений — это треугольник ABC (см. рис. 19). Проведем в нем высоту BD. Очевидно, что угол DBC равен α.

Выразим сторону BD из треугольника BCD:

(3.148)

Выразим сторону BD из треугольника ABD:

(3.149)

Приравняем (3.148) и (3.149):

(3.150)

Откуда находим время полета:

(3.151)

Выразим AD из треугольника ABD:

(3.152)

Выразим сторону DC из треугольника BCD:

(3.153)

Но Получаем

(3.154)

Подставим в это уравнение, полученное выражение для времени полета (3.151):

(3.155)

(3.156)

3.2.19. Как решать задачи с помощью закона движения? (по горизонтали)

Как правило, в школе при решении задач на равнопеременное движение применяются формулы (3.7), (3.8), (3.10)—(3.14). Однако такой подход к решению трудно применить к решению многих задач. Рассмотрим конкретный пример.

Опоздавший пассажир подошёл к последнему вагону поезда в тот момент, когда поезд тронулся, начав движение с постоянным ускорением Единственная открытая дверь в одном из вагонов оказалась от пассажира на расстоянии Какую наименьшую постоянную скорость он должен развить, чтобы успеть сесть в поезд?

Введем ось Ox, направленную вдоль движения человека и поезда. За нулевое положение примем начальное положение человека («2»). Тогда начальная координата открытой двери («1») L:

(3.157)

Дверь («1»), как и весь поезд, имеют начальную скорость равную нулю. Человек («2») начинает движение со скоростью

(3.158)

Дверь («1»), как и весь поезд, движется с ускорением a. Человек («2») движется с постоянной скоростью:

(3.159)

Закон движения и двери и человека имеет вид (3.26):

Подставим условия (3.157), (3.158) и (3.159) в (3.26) для каждого из движущихся тел:

(3.160)

(3.161)

Мы составили уравнение движения для каждого из тел. Теперь воспользуемся уже известным алгоритмом для нахождения места и времени встречи двух тел — нам нужно приравнять (3.160) и (3.161):

(3.162)

Откуда получаем квадратное уравнение для определения времени встречи:

(3.163)

Это квадратное уравнение. Оба его решения имеют физический смысл — наименьший корень, это первая встреча человека и двери (человек с места может побежать быстро, а поезд не сразу наберет большую скорость, так что человек может обогнать дверь), второй корень — вторая встреча (когда уже поезд разогнался и догнал человека). Но наличие обоих корней означает — человек может бежать и медленнее. Скорость будет минимальна, когда уравнение (3.163) будет иметь один единственный корень, то есть

(3.164)

Откуда находим минимальную скорость:

(3.165)

В таких задачах важно разобрать в условиях задачи: чему равны начальная координата, начальная скорость и ускорение. После этого составляем уравнение движения и думаем как дальше решать задачу.

3.2.20. Как решать задачи с помощью закона движения? (по вертикали)

Свободно падающее тело прошло последние 10 м за 0,5 с. Найти время падения и высоту, с которой упало тело. Сопротивлением воздуха пренебречь.

Для свободного падения тела справедлив закон движения (3.30):

(3.166) начальная координата:

(3.167) начальная скорость:

Подставим условия в закон движения:

(3.168)

Подставляя в уравнение движения (3.168) нужные значения времени, будем получать координаты тела в эти моменты.

В момент падения координата тела

(3.169)

За с до момента падения, то есть при координата тела

(3.170)

Уравнения (3.169) и (3.170) составляют систему уравнений, в которой неизвестны H и t_0. Решая эту систему получим:

(3.171)

(3.172)

Итак, зная вид закона движения (3.30), и используя условия задачи для нахождения и получаем закон движения для данной конкретной задачи. После чего, подставляя нужные значения времени, получаем соответствующие значения координаты. И решаем задачу!

Источник