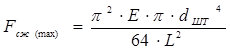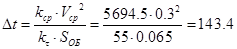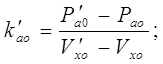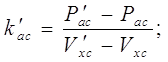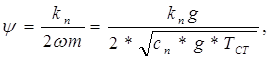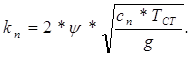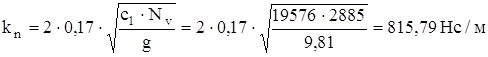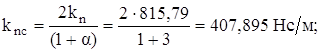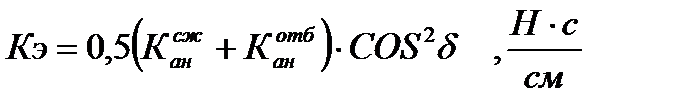Расчет параметров амортизатора
Расчет характеристики амортизатора
Для расчета параметров амортизатора с начало выбираем коэффициент апериодичности y=0,15…0,3, принимаем y=0,2.
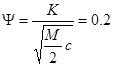
откуда коэф. сопротивления амортизатора
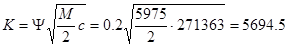
М – масса приходящаяся на подвеску, приведенная к центру колеса;
c=271363 H/м – жесткость подвески, приведенная к центру колеса;
Учитывая, что коэф. сопротивления на ходе отбоя 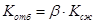
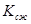
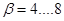
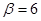
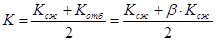
Определяем коэффициент сопротивления на ходе сжатия амортизатора:
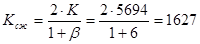
Определяем коэффициент сопротивления амортизатора на ходе отбоя:
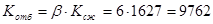
По известным коэффициентам строится характеристика амортизатора, в которой максимальная сила сопротивления: 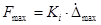
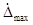
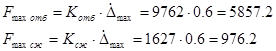
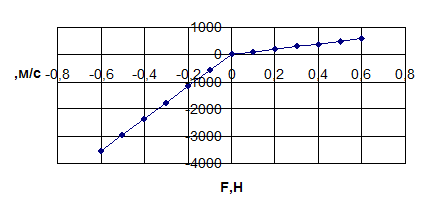
Рис. 4.1. Характеристика амортизатора
Расчет параметров амортизатора
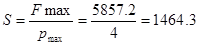
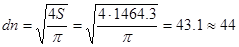
pmax=4 МПа – максимальное давление в амортизаторе;
Fmax= Fmax(отб)=5857.2 H – максимальная сила сопротивления амортизатора на ходе отбоя;
Определим диаметр штока (приняв его длину L= 300 мм)
Из расчета на устойчивость штока при максимальном осевом сжатии:
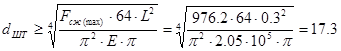
Площадь поршня на ходе отбоя
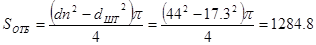
Площадь поршня на ходе сжатия
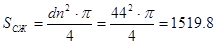
По ГОСТ выбираем амортизатор с диаметром кожуха: D=70 мм.
Гидравлический расчет амортизатора
Выбираем площадь сечения проходных отверстий такую, чтобы получить заданную характеристику.
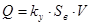
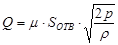
где 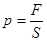
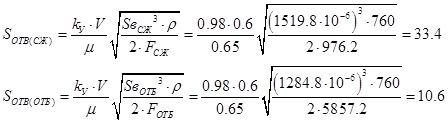
kУ=0.98 – коэф. утечек;
Sв=SвСЖ= 1519.8 мм2 – площадь вытеснителя на ходе сжатия;
Sв=SвОТБ= 1284.8 мм2 – площадь вытеснителя на ходе отбоя;
m=0.65 – коэф. расхода;
Тепловой расчет амортизатора
Мощность, рассеиваемая амортизатором в атмосферу
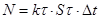
kt=55 Втм2/с – коэф. теплоотдачи;
Dt – перепад температур между поверхностью амортизатора и набегающим потоком воздуха;
Обдуваемая площадь поверхности амортизатора
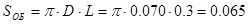
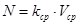
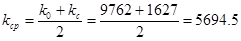
Vср=0,3 м/с – средняя скорость перемещения поршня.
Температура стенок амортизатора
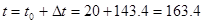
Расчет характеристики амортизатора
8 Расчет характеристики амортизатора
Амортизатор, предназначенный для гашения колебаний колес и кузова, повышает плавность хода автомобиля, устойчивость движения,
Долговечность упругих элементов и шин. Решающее влияние на все указанные выше качества автомобиля оказывает правильный выбор характеристики амортизатора, т.е. правильный выбор зависимости силы на штоке амортизатора от скорости относительного перемещения штока и цилиндра. Математически эта зависимость устанавливается уравнением:
Где Pa – сила на шток амортизатора;
Vn – скорость относительного перемещения штока и цилиндра амортизатора;
ka – коэффициент пропорциональности;
n – показатель степени, который обычно колеблется в пределах 1 – 2.
Конструктивно амортизатор в проектируемой подвеске располагается внутри направляющей пружинной стойки. Так как передаточное число iX=1,0112 близко к единице, то перемещение штока должно соответствовать величине, близкой к ходу колеса 150 мм.
На рис. 8.1 изображена линейная характеристика современного гидравлического амортизатора, которая обычно определяется следующими параметрами: коэффициентами сопротивления отбоя kao и сжатия kac при закрытых клапанах амортизатора; коэффициентами сопротивления k¢ao и k¢ac при открытых клапанах и силами на штоке амортизатора Рао и Рас, при которых открываются клапаны амортизатора.
Величины коэффициентов kao и kac определяются расчетом, исходя из требований к плавности хода или устойчивости движения автомобиля. Силы на штоке автомобиля могут быть определены по формулам:
Скорости относительного движения штока и цилиндра амортизатора Vx0 и Vxc, соответствующие моменту открытия клапанов, обычно лежат в пределах 0,3 – 0,52 м/с.
Величины коэффициентов k¢ao и k¢ac обычно не рассчитываются. Однако, если имеется экспериментально определенная характеристика, то они могут быть рассчитаны по формулам:
В большинстве конструкций амортизаторов показатель степени n не равен единице, однако характеристика амортизатора для инженерных расчетов приводится к линейной.
При выборе характеристики амортизатора, обычно, задаются величиной парциального коэффициента апериодичности, рассматривая подвеску как одномассовую систему:
где kn – приведенный коэффициент сопротивления амортизатора;
g – ускорение силы тяжести;
Cn – жесткость подвески;
ТСТ – статическая нагрузка на подвеску.
Диапазон коэффициента апериодичности y=0,15…0,30. Жесткость подвески c1=19576 Н/м (на одно колесо). Нагрузка на одно колесо Nv= 2885 Н. Принимая y=0,17, определяем kn:
При несимметричной характеристике необходимо, зная величину kn, установить приведенные коэффициенты сопротивления амортизатора при сжатии и отбое. С этой целью необходимо выбрать отношение a=kno/knc, которое для современных амортизаторов находится в пределах от 2 до 5. В этом случае принимая a=3, получим:
Действительные коэффициенты сопротивления амортизатора определяются из выражений:
где S – вертикальная деформация подвески;
fa – относительное перемещение поршня и цилиндра амортизатора.
Для данного случая dS/dfa является ни чем иным, как кинематическим передаточным числом подвески iX=1,0112.
kao=1223,685∙(1,0112) 2 =1251,25 Нс/м;
kac=407,895∙1,0112 2 =417,08 Нс/м.
Силы на штоке амортизатора:
где Vxo и Vxc – скорости относительного движения штока и цилиндра амортизатора при ходах отбоя и сжатия, соответствующие моменту открытия клапанов.
Из диапазона 0,3…0,52 м/с принимаем скорость Vxo=Vxc=0,5 м/с в связи с тем, что подвеска довольно жесткая для легкового автомобиля, имеет большой ход и воспринимает высокие нагрузки.
Pao=1251,25∙0,5=625,625 H»626 H.
Величины коэффициентов сопротивления амортизатора при открытых клапанах принимаем:
Относительная скорость перемещения штока и цилиндра V¢xo=V¢xc=0,8 м/с.
Столь низкие на первый взгляд демпфирующие силы и коэффициенты рассчитаны с учетом того, что в направляющей втулке амортизатора создаются достаточно высокие нагрузки, вызывающие силу трения, также являющуюся демпфирующей и которую нужно учитывать при выборе характеристики амортизатора.
По результатам расчета строим характеристику амортизатора.
Расчет характеристики амортизатора
8 Расчет характеристики амортизатора
Амортизатор, предназначенный для гашения колебаний колес и кузова, повышает плавность хода автомобиля, устойчивость движения,
Долговечность упругих элементов и шин. Решающее влияние на все указанные выше качества автомобиля оказывает правильный выбор характеристики амортизатора, т.е. правильный выбор зависимости силы на штоке амортизатора от скорости относительного перемещения штока и цилиндра. Математически эта зависимость устанавливается уравнением:
Где Pa – сила на шток амортизатора;
Vn – скорость относительного перемещения штока и цилиндра амортизатора;
ka – коэффициент пропорциональности;
n – показатель степени, который обычно колеблется в пределах 1 – 2.
Конструктивно амортизатор в проектируемой подвеске располагается внутри направляющей пружинной стойки. Так как передаточное число iX=1,0112 близко к единице, то перемещение штока должно соответствовать величине, близкой к ходу колеса 150 мм.
На рис. 8.1 изображена линейная характеристика современного гидравлического амортизатора, которая обычно определяется следующими параметрами: коэффициентами сопротивления отбоя kao и сжатия kac при закрытых клапанах амортизатора; коэффициентами сопротивления k¢ao и k¢ac при открытых клапанах и силами на штоке амортизатора Рао и Рас, при которых открываются клапаны амортизатора.
Величины коэффициентов kao и kac определяются расчетом, исходя из требований к плавности хода или устойчивости движения автомобиля. Силы на штоке автомобиля могут быть определены по формулам:
Скорости относительного движения штока и цилиндра амортизатора Vx0 и Vxc, соответствующие моменту открытия клапанов, обычно лежат в пределах 0,3 – 0,52 м/с.
Величины коэффициентов k¢ao и k¢ac обычно не рассчитываются. Однако, если имеется экспериментально определенная характеристика, то они могут быть рассчитаны по формулам:
В большинстве конструкций амортизаторов показатель степени n не равен единице, однако характеристика амортизатора для инженерных расчетов приводится к линейной.
При выборе характеристики амортизатора, обычно, задаются величиной парциального коэффициента апериодичности, рассматривая подвеску как одномассовую систему:
где kn – приведенный коэффициент сопротивления амортизатора;
g – ускорение силы тяжести;
Cn – жесткость подвески;
ТСТ – статическая нагрузка на подвеску.
Диапазон коэффициента апериодичности y=0,15…0,30. Жесткость подвески c1=19576 Н/м (на одно колесо). Нагрузка на одно колесо Nv= 2885 Н. Принимая y=0,17, определяем kn:
При несимметричной характеристике необходимо, зная величину kn, установить приведенные коэффициенты сопротивления амортизатора при сжатии и отбое. С этой целью необходимо выбрать отношение a=kno/knc, которое для современных амортизаторов находится в пределах от 2 до 5. В этом случае принимая a=3, получим:
Действительные коэффициенты сопротивления амортизатора определяются из выражений:
где S – вертикальная деформация подвески;
fa – относительное перемещение поршня и цилиндра амортизатора.
Для данного случая dS/dfa является ни чем иным, как кинематическим передаточным числом подвески iX=1,0112.
kao=1223,685∙(1,0112) 2 =1251,25 Нс/м;
kac=407,895∙1,0112 2 =417,08 Нс/м.
Силы на штоке амортизатора:
где Vxo и Vxc – скорости относительного движения штока и цилиндра амортизатора при ходах отбоя и сжатия, соответствующие моменту открытия клапанов.
Из диапазона 0,3…0,52 м/с принимаем скорость Vxo=Vxc=0,5 м/с в связи с тем, что подвеска довольно жесткая для легкового автомобиля, имеет большой ход и воспринимает высокие нагрузки.
Pao=1251,25∙0,5=625,625 H»626 H.
Величины коэффициентов сопротивления амортизатора при открытых клапанах принимаем:
Относительная скорость перемещения штока и цилиндра V¢xo=V¢xc=0,8 м/с.
Столь низкие на первый взгляд демпфирующие силы и коэффициенты рассчитаны с учетом того, что в направляющей втулке амортизатора создаются достаточно высокие нагрузки, вызывающие силу трения, также являющуюся демпфирующей и которую нужно учитывать при выборе характеристики амортизатора.
По результатам расчета строим характеристику амортизатора.
Перевод статьи о подвеске автомобиля. Часть 1
В койловерах применяются пружины сжатия. Для дальнейших рассуждений определимся с обозначениями пружин и основными их характеристиками:
Диаметр витка (Dw)
Диаметр «проволоки» из которой сделана пружина.
Средний диаметр пружины (Dm)
Диаметр пружины измеренный по оси «проволоки
«, из которой изготовлена пружина. Видно, что справедливо равенство: Dm = Di + Dw
Количество активных витков пружины (Na)
Количество активных витков пружины показывает какой количество витков воспринимает нагрузку. Обычно это число равно полному количеству витков пружины за минусом двух. Эти два витка, не дают вклада в общую жесткость пружины.
Формула расчета коэффициента жесткости пружины:
k = G * (Dw)^4 / 8 * Na * (Dm)^3
45 ГПа)
(небольшое отступление. в оригинале статьи использовали термин «torsional modulus»(модуль кручения), вместо термина модуль сдвига, это разные вещи). Модуль сдвига это отношение касательного напряжения к сдвиговой деформации, т.е. G = (действующая сила/площадь, на которую сила действует) / (смещение / начальная длинна). Формула немного сложная для понимания, но, если учесть, что модуль сдвига есть в таблицах и нет необходимости его высчитывать, то все встает на свои места. В исходном тексте статьи приведен пример, где G = 11250000psi, если перевести в Па, то получим 77,57ГПа (практически наша пружинная сталь, но в оригинале статьи упоминается какая то сталь без указания марки с повышенным содержанием хрома и углерода)
Дальше в оригинале статьи приводится табличка, в которой наглядно показано что как изменяется, при изменении членов этого уравнения. Мы тут все русские люди, изучавшие математику в школе и прекрасно понимающие как работают дроби, позвольте мне тут эту таблицу не приводить и так все понятно.
Точно так же, глядя на формулу мы видим, что увеличение диаметра при прочих одинаковых параметрах ведет к увеличению жесткости пружины и наоборот.
Таким образом можно для себя отметить важные моменты:
1. При заданных длине и диаметре пружины менее жесткая пружина будет иметь большее количество витков, и как следствие меньший ход. Т.е. для сохранения величины хода менее жесткую пружину необходимо делать выше.
2. При заданной жесткости пружины и ее высоте больший диаметр пружины (которая требуется для большего в диаметре амортизатора) будет иметь меньшее количество витков и как следствие больший ход.
Представленные на рынке пружины имеют разную высоту, диаметр и жесткость. Но при этом надо принять во внимание, что разница между 2,5″ и 3″ пружинами при одинаковой жесткости и высоте по остальным параметрам столь не значительна, что в этом случае диаметр не может являться основным фактором, на основе которого принимают решение о покупке того или иного варианта.
Практически жесткость пружины можно узнать непосредственно измерив соответствующие значения: (кг/мм) = Сила(кг)/Деформация(мм)
Жесткость пружины может быть постоянной величиной или переменной (имеется в виду зависимость от деформации). Пружины, которые не меняют свою жесткость от деформации получили название линейные ( * ) Также существуют пружины, которые изменяют свою жесткость в зависимости от деформации, это так называемые прогрессивные пружины. Как правило прогрессивные пружины имеют разный диаметр витков по высоте. Здесь мы не будем рассматривать такие пружины, т.к. в койловерах они не применяются.
( * )В действительности же, если мы начнем измерять жесткость линейной пружины, то в первые и последние 10% ее хода жесткость будет отливаться от остальных 80%. Этот момент так же приходится учитывать.
Высота в свободном состоянии (Lo)
Высота в свободном состоянии это измеренная высота пружины, на которую не действует нагрузка. Теоретически задается производителем при изготовлении пружины.
Существует зависимость количества витков пружины, которые можно изготовить от диаметра пружины. Например, слишком длинная пружина при небольшом диаметре не будет деформироваться под нагрузкой как задумано, что приведет к невозможности выполнять свои функции в полной мере. Именно по этой причине 18″ пружины диаметром 3″ существуют, а диаметром 2″ их нет.
Для создания пружины с различной высотой в свободном состоянии, но с одинаковой жесткостью производитель просто увеличивает расстояние между витками. Т.е. параметры: диаметр проволоки, из которой изготовлена пружина, диаметр витка и количество витков остаются без изменений, изменяется только высота в свободном состоянии.
При нормальной эксплуатации (т.е. при использовании пружины в условиях, которые предусматривал разработчик) высота пружины в свободном состоянии меняться не должна.
Высота в сжатом состоянии(Lc)
Высота в сжатом состоянии это высота,меньше которой пружина сжаться не в состоянии без ее разрушения. В этом состоянии витки пружины прижаты друг к другу.
Ход пружины (Sc)
Ход пружины это разница между высотой пружины в свободном состоянии и высотой пружины в сжатом состоянии.
Предельная нагрузка (Fc)
Предельная нагрузка это нагрузка, при превышении которой не происходит деформации пружины без ее разрушения. При приложенной предельной нагрузки к пружине измеряют высоту в сжатом состоянии. Именно предельная нагрузка вызывает смыкание витков пружины. Это очень важный параметр. Он говорит нам о том, какую максимальную нагрузку способна выдержать пружина вовремя своей работы. Без этой информации не обойтись при проектировании длинно ходовых подвесок, в которых необходимо сделать ход колеса максимальным.
Двойные пружины
Можно с уверенность сказать, что проектирование подвески это прежде всего поиск нужного баланса. С одной стороны пружина должна быть достаточно мягкая для перемещения по дорогам с большими ямами, выступами, хода подвески должно быть достаточно для компенсации перепадов рельефа. Пружина должна обеспечивать достаточный комфорт для перемещения по рельефу подобного типа. С другой стороны жесткость пружины должна быть достаточной для того, чтобы сохранить контроль при быстром движении по неровной дороге, прохождении поворотов, торможении и т.д. В общем жесткая пружина требуется именно тогда, когда мы говорим о скоростном перемещении.
Ki = (Km * Kt) / (Km + Kt)
Ki = суммарная начальная жесткость составной пружины
Km = жесткость мягкой пружины
Kt = жесткость жесткой пружины
Жесткость составной пружины, в случае, когда DRS уперлась в ограничительной кольцо, просто равняется жесткости жесткой пружины.
Примечание: в оригинале статьи введены понятие tender spring и main spring. Судя по фото main spring это мягкая пружина, tender spring это жесткая пружина. Но дальше в статье эти понятия были перепутаны, в частности в вышеприведенной формуле.
На этом про пружины хватить, определимся с некоторыми терминами и двинемся дальше:
Полная нагрузка колеса на поверхность (CW)
Усилие, с которым автомобиль давит на грунт одним из колес. Надо учесть, что это не просто общая масса автомобиля, поделенная на четыре. Данный параметр показывает распределение нагрузки автомобиля на поверхность.
Нагрузка от подрессоренной массы на одно колесо (CSW)
Нагрузка, которая приходится на каждую пружину. Так же как и предыдущий, указанный параметр показывает распределение нагрузки на подвеску.
Нагрузка от не подрессоренной массы на поверхность (CUW)
Нагрузка от не подрессоренной части автомобиля, приходящаяся на одно колесо. Можно сказать, что численно равно сумме масс: колеса в сборе, тормозному суппорту, половине массы моста, половине массы рычага, массе амортизатора и пружины.
Точка перехода(SUR)
Значение в процентах. Показывает в какой момент в составной пружине начинает работать жесткая часть.
SUR = Жесткость жесткой пружины / Жесткость составной пружины* 100% = (Kf / Ki) *100%
Возрастающая жесткость
Термин имеет отношение к элементам подвески, которые дают свой положительный вклад в жесткость, это могут быть, к примеру демпферы, пружины, подрессорные листы и т.д. Термин известен, как прогрессирующая жесткость.
Уменьшающаяся жесткость
Как не трудно догадаться это полная противоположность возрастающей жесткости. Т.е. есть элементы, жесткость которых падает по мере хода подвески. Термин известен как регрессирующая жесткость.
Дальше мы будем говорить как раз об углах, размерностях и взаимном положении отдельных элементов подвески.
Расчет амортизаторов
5.1 Цель работы: изучить методику расчета характеристик амортизатора и определение его геометрических параметров.
5.2 Теоретическая часть
Устройство, гасящее колебание в подвеске и называемое амортизатором, совместно с трением в подвеске создаёт силы сопротивления колебаниям автомобиля и переводит механическую энергию колебаний в тепловую. На автомобилях широко применяются гидравлические амортизаторы двухстороннего действия: рычажные и телескопические. Телескопические амортизаторы легче рычажных, имеют более развитую поверхность охлаждения, работают при меньших давлениях (2,5 – 5,0 МПа), технологичнее в производстве. В силу указанных преимуществ они получили широкое распространение на отечественных и зарубежных автомобилях.
Быстрота затухания колебаний при работе упругих элементов подвески достигается созданием достаточно большой силы Рс сопротивления колебаниям. Эта сила создается межлистовым трением рессор, трением в шарнирах подвески и в основном сопротивлением амортизаторов. В первом приближении силу Рс можно считать пропорциональной скорости V колебаний кузова относительно колеса:
В теории автомобиля оценку затухания колебаний производят по относительному коэффициенту затухания:

где с=P0/f – жесткость подвески, Н/см;
У современных автомобилей колебания кузова происходят с затуханием, соответствующим y=0,15¸0,35. Для сохранения заданной степени затухания колебаний в подвеске с уменьшением её жёсткости сопротивление амортизаторов также следует уменьшать.

где Рр – вес подрессорной части, приходящейся на колесо в статическом положении, Н;
При заданном эквивалентном коэффициенте сопротивления колебаниям Кэ коэффициент Ка сопротивления амортизатора зависит от его типа и расположения относительно колеса.

Усилия в амортизаторе Ра определяются для телескопического амортизатора, установленного под углом:
Зависимость силы на штоке амортизатора от скорости относительно перемещения штока и цилиндра рассчитывается в общем случае по формулам:

а) На начальном участке:
где: Рн – сила на штоке амортизатора на начальном участке, Н;
Vn – скорость поршня, см/с;
Кан – коэффициент сопротивления амортизатора на начальном участке до открытия клапана, Н с/см;
n – показатель степени, принимаемый при инженерных расчетах n=1.

б) на клапанном участке:
где: Рн – сила сопротивления амортизатора в момент открытия клапана, Н;
Кан – коэффициент сопротивления амортизатора на клапанном участке, Н с/см ;
V¢n – критическая скорость поршня, соответствующая открытию клапана, V¢n=20¸30 см/с, причем последняя цифра характеризует весьма напряженный режим.
Скорость поршня Vn принимается в расчетах равной 50…60 см/с. При значительной скорости колебаний на ходе сжатия и отбоя открываются разгрузочные клапаны (т. 1 и 2 характеристики амортизатора).
Для двухстороннего амортизатора:


Для проведения расчетов, данные берем из таблицы 3 (приложение).
Определим эквивалентный коэффициент по формуле 5.2.
Далее определяем по формуле 5.2, коэффициент сопротивления амортизатора при сжатии.
Отсюда определим коэффициент сопротивления амортизатора при отбое:
Находим силу сопротивления амортизатора в момент открытия клапанов:
Далее найдем Рсжк и Ротбк по формулам:

При выборе основных размеров амортизатора пользуются расчетной мощностью Nрасч, с учетомкритической скорости поршня, соответствующей открытию клапана. Мощность, поглощаемую амортизатором, можно подсчитать по формуле:
Зная расчетную мощность амортизатора, можно рассчитать работу L, поглощенную амортизатором за время τ = 1 час и перешедшую в тепло:
Диаметр рабочего цилиндра амортизатора определяется по формуле:
где Рам – давление в амортизаторе, равное (2,5-5,0)*10 Па;
Fвн – площадь по внутреннему диаметру стенки амортизатора, равная:
Fш – площадь в сечении по штоку, равная:
Наружный диаметр амортизаторов:
где δ – толщина стенки, равная 2,55 мм.
Конструктивную длину амортизатора (ход поршня) найдем по формуле:
Далее проведем расчет амортизатора на прочность.
Запас прочности по напряжениям изгиба: σs =στ=1600Мпа; σmax =700 Мпа,
Запас прочности по напряжениям кручения: τs= ττ =700 Мпа; τmax =50Мпа,
Тогда общий запас прочности будет:

Рисунок 5.2 – Амортизатор и его основные параметры
5.4 Содержание отчета
5.4.1 Согласно своему варианту (таблица 3, приложение) провести расчеты.
5.4.2 По окончании расчета сделать выводы по запасу прочности и схематично представить амортизатор по примеру рисунка 5.2.
Практическая работа №6 (2 часа)