Расчет дифференциала
Методические указания к практическим занятиям по курсу
Требования к конструкции подвижного состава
для студентов специальности 190701.01 Организация перевозок и управление на транспорте (Автомобильный транспорт)
Составители А. В. Буянкин
Рассмотрены и утверждены
на заседании кафедры
Протокол №78 от 07.02.2008
Рекомендованы к печати
Протокол №78 от 07.02.2008
хранится в библиотеке
главного корпуса ГУ КузГТУ
Общие положения
Цель курса Требования к конструкции подвижного состава – дать студентам инженерные знания, необходимые для объективной оценки конструкций автотранспортных средств (АТС), их агрегатов и систем.
В данном курсе решаются следующие задачи:
знакомство с основными требованиями к конструкциям АТС, их агрегатов и систем, изучение выходных и оценочных параметров агрегатов и систем АТС;
изучение условий эксплуатации и нагрузочных режимов агрегатов и систем АТС;
изучение рабочих процессов агрегатов и систем АТС, оценка влияния конструктивных и эксплуатационных факторов на рабочие процессы и выходные параметры агрегатов и систем АТС;
знакомство с основами расчета агрегатов и систем АТС на прочность и долговечность.
При изучении данного курса необходимо в первую очередь рассмотреть требования, предъявляемые к конструкции агрегатов и систем АТС, и проанализировать, как эти требования выполняются в существующих конструкциях. Основное внимание следует уделить изучению рабочих процессов и выходных параметров агрегатов и систем АТС. При этом необходимо выделить связи между рабочими процессами, нагрузочными режимами и требованиями к конструкции, а также отметить влияние конструктивных и эксплуатационных факторов на рабочие процессы и выходные параметры агрегатов и систем АТС.
Проектирование трансмиссии автомобиля обычно осуществляется в такой последовательности: в зависимости от назначения автомобиля определить принципиальную схему трансмиссии, рассмотреть основные характеристики, выбрать принципиальные схемы агрегатов, провести их конструирование и выполнить расчеты на прочность основных деталей. При этом конструктор анализирует существующие конструкции, оценивает их конструктивные, производственные и эксплуатационные достоинства и недостатки, учитывает преемственность, особенности производства и возможности широкой унификации между существующими и проектируемыми образцами.
1 Расчет дифференциала
Дифференциал – механизм, распределяющий подводимый к нему крутящий момент между выходными валами и обеспечивающий их вращение с неодинаковыми угловыми скоростями.
Классификация и требования к дифференциалам подробно рассмотрены в [3, 4, 5].
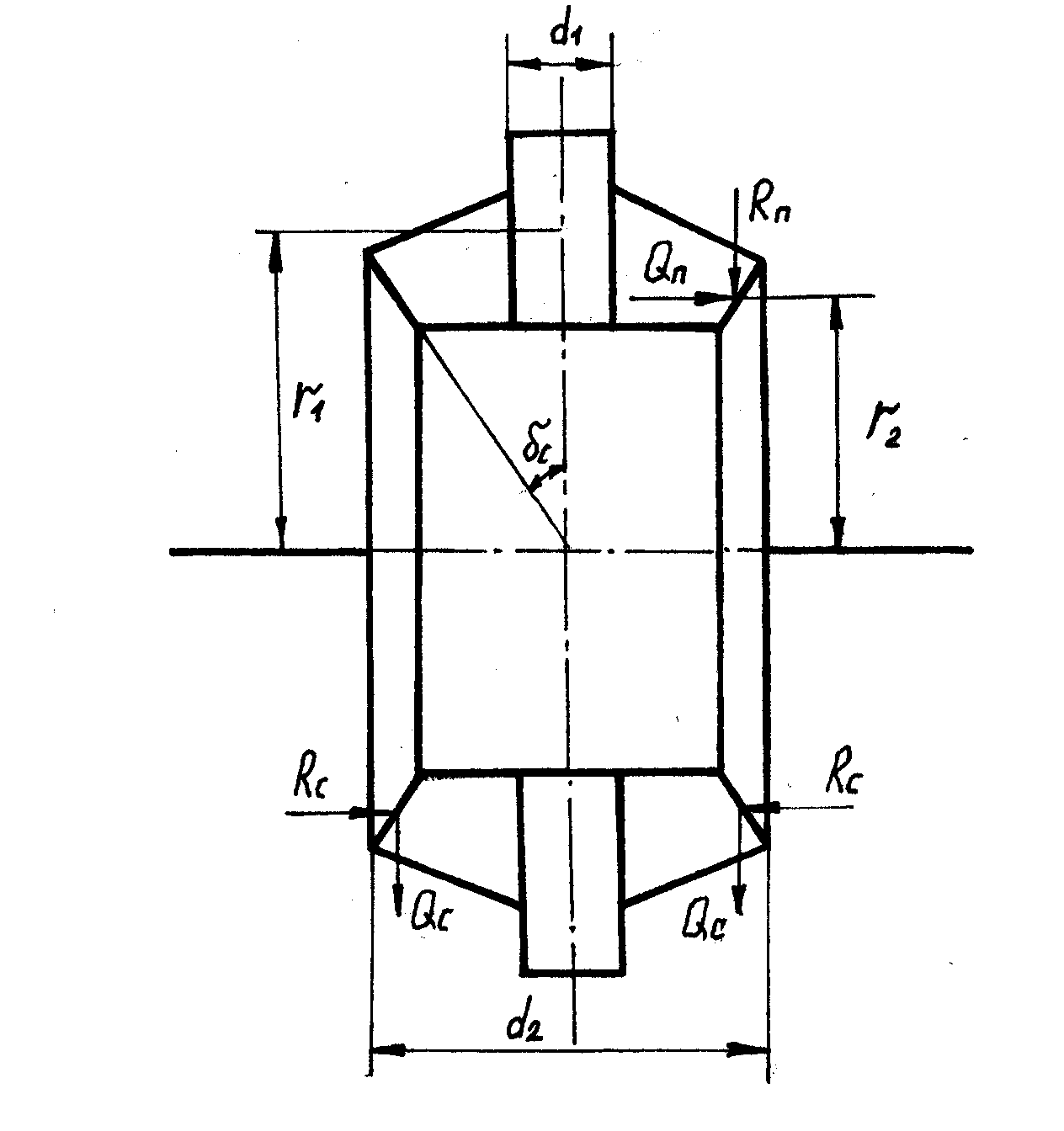
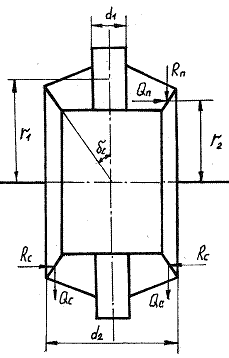
На современных автомобилях наибольшее распространение получили симметричные конические дифференциалы (рисунок 1.1). Такие дифференциалы, называемые часто простыми, применяются как на легковых, так и на грузовых автомобилях, причем как в качестве межколесных, так и в качестве межосевых.
Рисунок 1.1 – Расчетная схема симметричного конического дифференциала
Сателлиты и полуосевые шестерни выполняются прямозубыми. Число зубьев сателлитов и шестерен может быть как четным, так и нечетным, но по условиям сборки должно подчиняться условию:

где 

Шип крестовины под сателлитом испытывает напряжения смятия и среза.
Напряжения смятия , Па, рассчитывают по формуле

где 

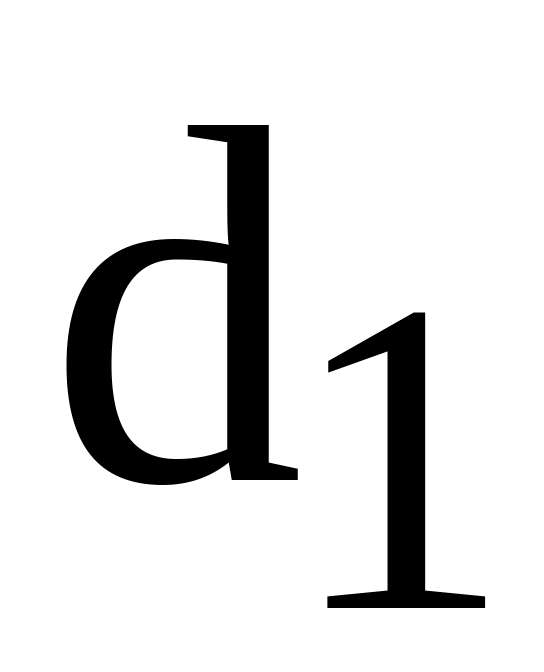
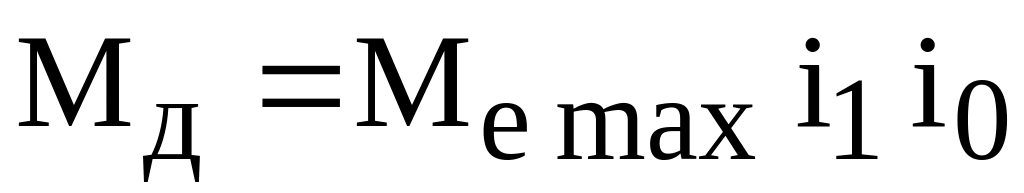
где 


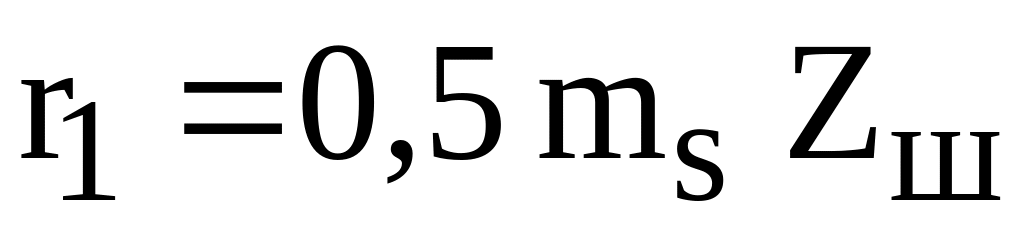
где 

где 
Допустимое давление между шипами и сателлитами дифференциалов [5]:
легковых автомобилей – = 80 МПа;
грузовых автомобилей – = 100 МПа.
Длина оси l, м, на которой вращается сателлит, может быть приближенно определена по формуле

где b – ширина зубчатого венца сателлита, м; 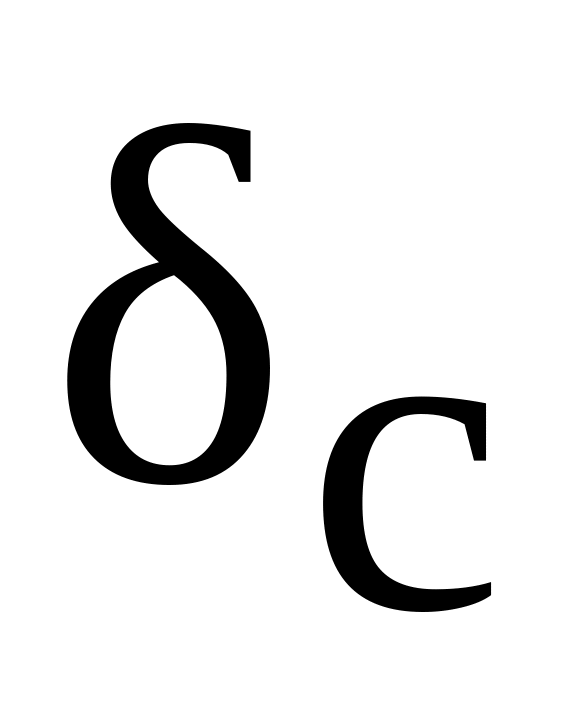

где 
Допустимые напряжения смятия – [] = 50 60 МПа [4].
Напряжение среза 

Допустимые напряжения среза – [ ] = 100 120 МПа [4].
Радиальные силы в симметричном дифференциале уравновешиваются, осевые воспринимаются корпусом дифференциала.
Торцы сателлитов рассчитывают на смятие под действием осевой силы. Осевую силу 

где 
Угол зацепления – = 20 [5].
Радиус приложения окружной силы в зацеплении при расчетах можно принять равным радиусу приложения осевой силы, действующей на ось сателлита.
Напряжение смятия 

где 
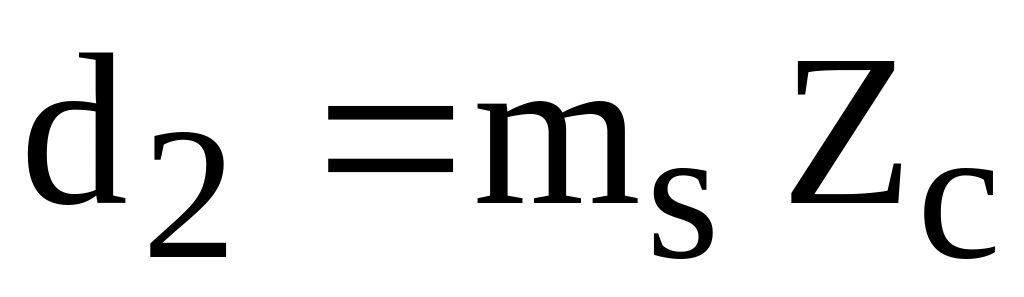
Допустимые напряжения смятия – [ ] = 10 20 МПа [4].
Торцы полуосевых шестерен рассчитывают на смятие под действием осевой силы, действующей на полуосевую шестерню.
Осевую силу 

Напряжение смятия торца полуосевой шестерни 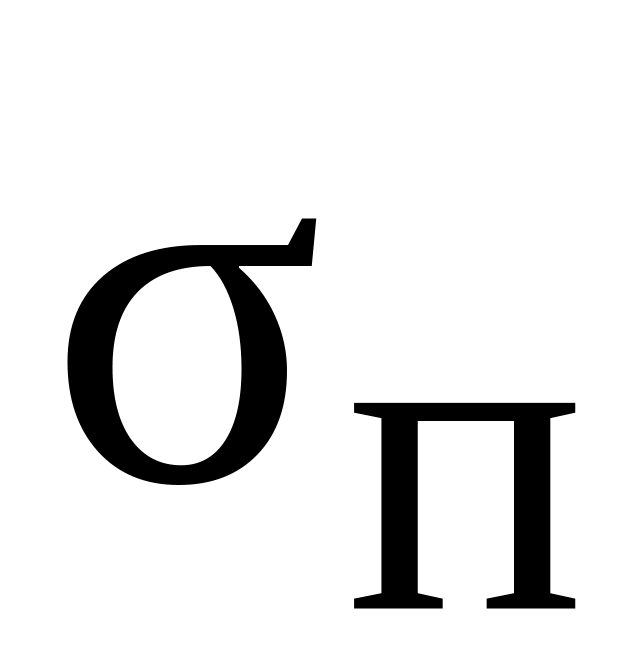

где 

Наибольший радиус торцовой поверхности шестерни может быть принят равным радиусу приложения осевой силы, действующий на ось сателлита.
Наименьший радиус торцовой поверхности шестерни приближенно может быть определен по формуле

где 
Минимальные диаметры полуосей приведены в таблице 1.2 [5].
Таблица 1.2 – Минимальные диаметры полуосей
Расчет основных элементов дифференциала
Сателлиты и полуосевые шестерни симметричного конического дифференциала выполняются прямозубыми.
Число зубьев сателлитов и шестерен может быть как четным, так и нечетным, но по условиям сборки должно подчиняться условию:
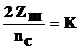
Шип крестовины под сателлитом испытывает напряжения смятия и среза.

где 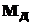


Момент на корпусе межколесного дифференциала автомобиля с колесной формулой 4 
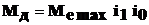
Радиус приложения осевой силы, действующей на ось сателлита, определяют по формуле:

где 
Диаметр шипа крестовины рассчитывают по формуле:
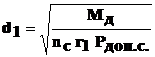
где 
Допустимое давление между шипами и сателлитами дифференциалов легковых автомобилей – 

Допустимые напряжения смятия – [s] = 50 ¸ 60 МПа.
Напряжение среза оси сателлита определяют по формуле:
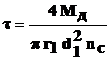
Допустимые напряжения среза – [ 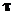
Радиальные силы в симметричном дифференциале уравновешиваются, осевые воспринимаются корпусом дифференциала.
Торцы сателлитов рассчитывают на смятие под действием осевой силы. Осевую силу определяют по формуле:
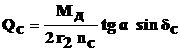
где 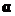
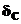

Половину угла начального конуса сателлита рассчитывают по формуле:

где 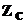
Радиус приложения окружной силы в зацеплении при расчетах можно принять равным радиусу приложения осевой силы, действующей на ось сателлита.
Напряжение смятия торца сателлита рассчитывают по формуле:
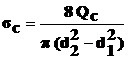
где 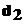
Диаметр торцевой поверхности сателлита, воспринимающей осевую нагрузку, определяют по формуле:
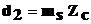
Допустимые напряжения смятия – [ 
Торцы полуосевых шестерен рассчитывают на смятие под действием осевой силы, действующей на полуосевую шестерню.
Осевую силу, действующую на полуосевую шестерню, определяют по формуле:

Напряжение смятия торца полуосевой шестерни рассчитывают по формуле:

где 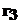

Допустимые напряжения смятия – [ 
Нагрузку на зубья сателлитов и полуосевых шестерен определяют из условия, что окружная сила распределена поровну между всеми сателлитами и каждый сателлит передает усилие двумя зубьями. Расчетный момент на сателлите и на полуосевой шестерне рассчитывают по формуле:
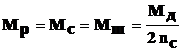
Расчет зубьев зубчатых колес дифференциала по напряжениям изгиба производят по формулам для конических главных передач. Допустимые напряжения изгиба зубьев – [ 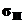
При повороте число оборотов сателлита на оси невелико ( 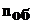
ПОЛУОСИ
Дата добавления: 2018-02-28 ; просмотров: 974 ; Мы поможем в написании вашей работы!
РАСЧЕТ ДИФФЕРЕНЦИАЛА
Дата добавления: 2015-01-16 ; просмотров: 6572 ; Нарушение авторских прав
Дифференциал – механизм, распределяющий подводимый к нему крутящий момент между выходными валами и обеспечивающий их вращение с неодинаковыми угловыми скоростями.
Классификация и требования к дифференциалам подробно рассмотрены в [3, 4, 5].
На современных автомобилях наибольшее распространение получили симметричные конические дифференциалы (рисунок 1.1). Такие дифференциалы, называемые часто простыми, применяются как на легковых, так и на грузовых автомобилях, причем как в качестве межколесных, так и в качестве межосевых.
Рисунок 1.1 – Расчетная схема симметричного конического дифференциала
Сателлиты и полуосевые шестерни выполняются прямозубыми. Число зубьев сателлитов и шестерен может быть как четным, так и нечетным, но по условиям сборки должно подчиняться условию:

Шип крестовины под сателлитом испытывает напряжения смятия и среза.
Напряжения смятия s, Па, рассчитывают по формуле

где 


Момент на корпусе 

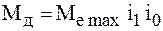
где 


Радиус приложения осевой силы 

где 
Диаметр шипа крестовины 

где 
Допустимое давление между шипами и сателлитами дифференциалов [5]:
· легковых автомобилей – 
· грузовых автомобилей – 
Длина оси l, м, на которой вращается сателлит, может быть приближенно определена по формуле

где b – ширина зубчатого венца сателлита, м; 
Половину угла начального конуса сателлита 

где 
Допустимые напряжения смятия – [s] = 50 ¸ 60 МПа [4].
Напряжение среза 

Допустимые напряжения среза – [ 
Радиальные силы в симметричном дифференциале уравновешиваются, осевые воспринимаются корпусом дифференциала.
Торцы сателлитов рассчитывают на смятие под действием осевой силы. Осевую силу 

где 
Угол зацепления – a = 20° [5].
Радиус приложения окружной силы в зацеплении при расчетах можно принять равным радиусу приложения осевой силы, действующей на ось сателлита.
Напряжение смятия 

где 
Диаметр торцевой поверхности сателлита 

Допустимые напряжения смятия – [ 
Торцы полуосевых шестерен рассчитывают на смятие под действием осевой силы, действующей на полуосевую шестерню.
Осевую силу 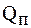

Напряжение смятия торца полуосевой шестерни 

где 

Наибольший радиус торцовой поверхности шестерни может быть принят равным радиусу приложения осевой силы, действующий на ось сателлита.
Наименьший радиус торцовой поверхности шестерни приближенно может быть определен по формуле

где 
Минимальные диаметры полуосей приведены в таблице 1.2 [5].
Таблица 1.2 – Минимальные диаметры полуосей
| Автомобиль | ВАЗ-2101 | Москвич-2140 | ГАЗ-24 | ГАЗ-53А | МАЗ-500А |
 , мм , мм | 21,6 | 24,0 | 27,5 | 42,0 | 42,0 |
Продолжение табл. 1.2
| Автомобиль | Урал-375Н | ЗИЛ-130 | КрАЗ-257 | БелАЗ-540А |
 , мм , мм | 48,0 | 48,0 | 58,0 | 58,0 |
Допустимые напряжения смятия – [ 
При повороте число оборотов сателлита на оси не превышает 
Нагрузку на зубья сателлитов и полуосевых шестерен определяют из условия, что окружная сила распределена поровну между всеми сателлитами и каждый сателлит передает усилие двумя зубьями.
Расчетный момент на сателлите и на полуосевой шестерне, рассчитывают по формуле

Расчет зубьев зубчатых колес дифференциала по напряжениям изгиба производят по формулам для конических главных передач. Допустимые напряжения изгиба зубьев – [ 
При выборе основных параметров зубчатых колес симметричных конических дифференциалов могут быть использованы данные таблицы 1.1 [5].
Таблица 1.1 – Геометрические параметры симметричных конических дифференциалов
| Автомобиль | Число зубьев | Внешний окружной модуль, мм | Конусное расстояние, мм | Угол профиля | Ширина венца, мм | Число сателлитов |
| сателлитов | шестерен | |||||
| ЗАЗ-968 | 3,50 | 39,13 | 20°30¢ | 11,0 | ||
| Москвич-2140 | 4,13 | 35,53 | 22°30¢ | 12,6 | ||
| ВАЗ-2101 | 4,0 | 37,77 | 22°30¢ | 12,0 | ||
| ГАЗ-24 | 5,0 | 47,20 | 23°30¢ | ––– | ||
| УАЗ-469 | 4,75 | 44,90 | 22°30¢ | 35,0 | ||
| ГАЗ-53А | 5,75 | 62,62 | 22°30¢ | 21,0 | ||
| ЗИЛ-130 | 6,35 | 78,09 | 22°30¢ | 27,0 | ||
| Урал-375 Н | 6,35 | 78,09 | 20° | 27,0 | ||
| КамАЗ-5320 | 6,35 | 78,09 | 22°30¢ | 27,0 | ||
| МАЗ-5335 | 5,50 | 62,77 | 20° | 22,5 | ||
| КрАЗ-257Б1 | 8,0 | 98,39 | 20° | 30,2 | ||
| БелАЗ-540А | 8,0 | 98,39 | 20° | 30,2 | ||
| БелАЗ-548А | 9,0 | 110,68 | 20° | 37,0 |
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Бочаров Н. Ф. Конструирование и расчет машин высокой проходимости: учебник для втузов / Н. Ф. Бочаров, И. С. Цитович, А. А. Полунгян. – М.: Машиностроение, 1983. – 299 с.
2. Бухарин Н. А. Автомобили. Конструкция, нагрузочные режимы, рабочие процессы, прочность агрегатов автомобиля: учеб. пособие для вузов / Н. А. Бухарин, В. С. Прозоров, М. М. Щукин. – М.: Машиностроение, 1973. – 504 с.
3. Лукин П. П. Конструирование и расчет автомобиля: учебник для студентов втузов / П. П. Лукин, Г. А. Гаспарянц, В. Ф. Родионов. – М.: Машиностроение, 1984. – 376 с.
4. Осепчугов В. В. Автомобиль: Анализ конструкции, элементы расчета: учебник для студентов вузов / В. В. Осепчугов, А. К. Фрумкин. – М.: Машиностроение, 1989. – 304 с.
5. Проектирование трансмиссий автомобилей: Справочник / А. И. Гришкевич [и др.]. – М.: Машиностроение, 1984. – 272 с.