Расчет допустимой нагрузки на ось тягача и полуприцепа
В сфере грузоперевозок важно не только верно подобрать автомобиль, но и тщательно просчитать перед отправкой в рейс ряд параметров. Один из них – допустимая нагрузка на ось тягача. Предварительный расчет осевых нагрузок на груженый полуприцеп с тягачом поможет избежать штрафов и неприятностей на пунктах контроля.
В статье разберем алгоритмы ручных и онлайн-подсчетов, рассмотрим санкции за перегрузы.
Для чего нужен расчет допустимой нагрузки на ось
Рассчитать нагрузку на ось тягача и полуприцепа перед выездом – залог спокойного пути и прохождения весового контроля. Законодательство РФ вводит ограничения на эти значения. Именно оси грузовиков и фур передают дорожному покрытию нагрузки. Предельные показатели попросту разрушают асфальт.
Чтобы дорожное полотно оставалось в целости и сохранности, для каждого типа автомобилей предусмотрены свои допустимые показатели. Значения детально описаны во втором приложении к Постановлению Правительства под номером 272.
Обхитрить сотрудников дорожной службы не выйдет: близ заездов в города установлены пункты весового контроля. Через них «прогоняют» все фуры, после чего всплывают перегрузы, и назначаются солидные штрафы. Чтобы сохранить наличные и нервы, рассчитать риски нужно заранее.
Методика расчета
Вести подсчет можно несколькими способами: вычислять данные через формулы или внести значения в калькулятор нагрузки на ось тягача и полуприцепа. На онлайн-программе мы остановимся позже, пока же разберем методику самостоятельных расчетов.
Для тягача
Здесь дела обстоят просто: нагрузка на ведущую ось пустого седельного тягача прописана в ПТС. Если документ находится не под рукой, данные для разных моделей тягачей («Вольво», «Мерседес») представлены в открытом доступе.
Для тягача с полуприцепом
Здесь многое зависит от веса самого автомобиля. Нагрузка на оси и вес грузовика (скотовоза, цистерны, фуры) заключается в следующем:
масса (m) равна нагрузке на переднюю ось (A) плюс нагрузка на каждую из осей (N).
M = нагрузка A +нагрузка N + нагрузка N1, N2, N3, N4, N5.
Для тягача с груженым полуприцепом
Определять данные для груженой фуры самостоятельно довольно сложно. Дело не в формуле, а в нюансах, которые влияют на результат.
Для получения достоверных значений подвеска фуры должна быть неизношенной, балансировка колес настроена корректно, прицеп не должен прогибаться под весом товара, а площадь, на которую «ложится» вес, обязательно должна быть ровная.
Если все перечисленные пункты соблюдены, подсчет будет таким:
Первым делом высчитываем нагрузку на прицеп.
75 процентов от M2+M3. Допустим, масса тягача = 8 тоннам, прицепа – 10 тоннам, товар весит 20 тонн.
Выходит: (10+20)*0,75. Получаем 22,5 тонны нагрузки на полуприцеп.
Далее считаем нагрузку на каждую из осей фуры. Допустим, их в автомобиле три штуки.
Получаем: 22,5 тонны делим на 3. Итог – 7,5 тонн веса на каждую ось прицепа.
Следующим шагом вычисляем нагрузку на ось тягача. На этот показатель приходится 0,25 процента от массы прицепа и тягача.
Теперь нужно понять, какая часть веса приходится на задние оси. На них ложится 75 процентов от нагрузки на сам грузовик:
Нагрузка на переднюю ось: 15,5–5,8*2=3,9 тонны.
Подводим итог: максимальные нагрузки в нашем примере получаются: 3,9 тонны на переднюю ось, по 5,8 тонны на каждую из задних осей.
Что понадобится для расчета
Для подсчетов вам будет достаточно следующих параметров:
Распределение нагрузки на задние оси полуприцепа
Перед тем как приступить к расчетам, важно понимать принцип распределения веса на каждую из осей транспортного средства. На передние оси приходится только 25 процентов массы. Это объясняется тем, что «первые» оси держат лишь массу тягача и части полуприцепа. Весь остальной вес (75 процентов) ложится на задние оси (именно они фиксируют груженный товаром прицеп).
Как пользоваться калькулятором
Для удобства дальнобойщиков и транспортных компаний в Сети представлены онлайн-калькуляторы для определения нагрузок на оси. Данные сервисов, по отзывам на форумах, могут иметь незначительные погрешности. Но примерные значения в программах подбить вполне реально.
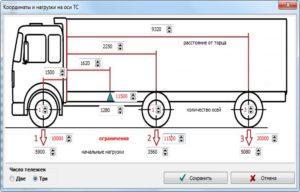
Здесь можно рассчитать нагрузки на каждый тип грузового транспорта.
Для этого вам нужно:
Программа представит результаты для каждой оси ТС. После данные можно распечатать.
Ответственность за перегруз
Если по какой-то причине подсчеты не были проведены, а весовой контроль показал перегруз, будьте готовы понести финансовое взыскание:
Точная сумма наказания зависит от размера превышенного веса.
Нужно понимать, что перегруз не только портит асфальт и опустошает вам кошелек.
Грузовик с неравномерной нагрузкой на оси движется рывками. Это создает неудобства шоферу и остальным участникам движения. Перегрузки негативно сказываются на ТС: детали быстрее приходят в негодность. Кроме того, большие массы изменяют длину тормозного пути, что нередко влечет за собой ДТП.
Итак, для спокойствия водителя и сохранности содержимого кошелька важно рассчитать нагрузку на оси грузовика. Это можно сделать вручную или с помощью онлайн-программ.
Учитывайте грузовые оси на полуприцеп. В формуле есть деление на задние и передние оси. Нагрузка на них распределяется как 75 процентов к 25 процентам. При подсчете обязательно учитывайте этот нюанс.
За перегрузы законодательство предусматривает немалые штрафы. Если при прохождении весового контроля вас поймают на перевесе, минимальная сумма взыскания составит 2 тысячи рублей для водителя.
В некоторых случаях дорожная инспекция может разрешать перегруз, но перед рейсом компания получает на это специальное разрешение.
Детальная информация видна на видео:
Расчет нагрузки на ось грузового автомобиля с полуприцепом
| Год выпуска | Тягач | Вес на рулевой оси 1. кг | Вес на ведущей оси 2. кг | % на ведущую ось | Масса с топливом. кг | Масса без топлива | Топлива в баках. литр | Вес топлива. кг |
|---|---|---|---|---|---|---|---|---|
| 2008 | Mercedes Actros 1841 | 5700 | 2480 | 30,3% | 8180 | 7760 | 500 | 420 |
| 2013 | Volvo FH | 5560 | 2240 | 28,7% | 7800 | 7254 | 650 | 546 |
| 2011 | MAN TGX18.400 | 5450 | 2240 | 29,7% | 7750 | 7355 | 470 | 395 |
| 2014 | DAF XF.105 | 5550 | 2350 | 29,7% | 7900 | 7450 | 450 | 536 |
Взвешиваем тягач с полуприцепом без груза
| Тягач | Полуприцеп | Топливо. литр | Вес топлива. кг | Вес на оси 1 | Вес на оси 2 | Вес на оси 3 | Вес на оси 4 | Вес на оси 5 | Вес сцепки с топливом. кг | Вес сцепки без топлива. кг | Нагрузка ССУ от полуприцепа. кг | Вес полуприцепа | Масса груза |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mercedes Actros 1841 | Fliegl SDS 350 | 400 | 336 | 5900 | 3560 | 1760 | 1800 | 1560 | 14916 | 14580 | 1280 | 6400 | 0 |
| MAN TGX18.400 | SCHMITZ SRR24 | 600 | 504 | 5300 | 3600 | 1900 | 1900 | 1900 | 15104 | 14600 | 1150 | 6850 | 0 |
Свои пожелания и отзывы о нашем калькуляторе нагрузок на оси направляйте нам по электронной почте info@vdnk.ru будем очень признательны.
Экспедитор или перевозчик? Три секрета и международные грузоперевозки
Экспедитор или перевозчик: кого предпочесть? Если перевозчик хороший, а экспедитор – плохой, то первого. Если перевозчик плохой, а экспедитор – хороший, то второго. Такой выбор прост. Но как определиться, когда хороши оба претендента? Как выбрать из двух, казалось бы, равноценных вариантов? Дело в том, что варианты эти не равноценны.
Страшные истории международных перевозок
МЕЖДУ МОЛОТОМ И НАКОВАЛЬНЕЙ.
Непросто жить между заказчиком перевозки и очень хитро-экономным владельцем груза. Однажды мы получили заказ. Фрахт на три копейки, дополнительные условия на два листа, сборник называется. В среду погрузка. Машина на месте уже во вторник, и к обеду следующего дня склад начинает неспешно закидывать в прицеп все, что собрал ваш экспедитор в адрес своих заказчиков–получателей.
ЗАКОЛДОВАННОЕ МЕСТО – ПТО КОЗЛОВИЧИ.
По легендам и на опыте, все, кто возил грузы из Европы автотранспортом, знают, каким страшным местом является ПТО Козловичи, Брестской таможни. Какой беспредел творят белорусские таможенники, придираются всячески и дерут втридорога. И это правда. Но не вся.
КАК ПОД НОВЫЙ ГОД МЫ ВЕЗЛИ СУХОЕ МОЛОКО.
Загрузка сборным грузом на консолидационном складе в Германии. Один из грузов – сухое молоко из Италии, доставку которого заказал Экспедитор. Классический пример работы экспедитора-«передатчика» (он ни во что не вникает, только передает по цепочке).
Документы для международных перевозок
Международные автомобильные перевозки грузов очень заоргонизованы и обюрокрачены, следствие – для осуществления международных автомобильных перевозок грузов используется куча унифицированных документов. Неважно таможенный перевозчик или обыкновенный — без документов он не поедет. Хоть это и не очень увлекательно, но мы постарались попроще изложить назначение этих документов и смысл, который они имеют. Привели пример заполнения TIR, CMR, T1, EX1, Invoice, Packing List.
Расчет нагрузки на ось для грузовых автоперевозок
Цель — исследование возможности перераспределения нагрузок на оси тягача и полуприцепа при изменении расположения груза в полуприцепе. И применение этого знания на практике.
Ты почему не ешь мухоморы? Таможня выдохнула грусть.
Что происходит на рынке международных автомобильных перевозок? ФТС РФ запретила оформлять книжки МДП без дополнительных гарантий уже нескольких федеральных округах. И уведомила о том, что с 1 декабря текущего года и вовсе разорвет договор с IRU как несоответствующим требованиям Таможенного союза и выдвигает недетские финансовые претензии.
IRU в ответ: «Объяснения ФТС России касательно якобы имеющейся у АСМАП задолженности в размере 20 млрд. рублей являются полнейшим вымыслом, так как все старые претензии МДП были полностью урегулированы. Что думаем мы, простые перевозчики?
Stowage Factor Вес и объем груза при расчете стоимости перевозки
Расчет стоимости перевозки зависит от веса и объема груза. Для морских перевозок чаще всего решающее значение имеет объем, для воздушных – вес. Для автомобильных перевозок грузов значение играет комплексный показатель. Какой параметр для расчетов будет выбран в том или ином случае – зависит от удельного веса груза (Stowage Factor).
Методика расчета нагрузки на ось для грузовых автоперевозок
Тяга к знаниям — она как «старость», в самый неожиданный момент может настичь любого. Вот и мы, застигнутые врасплох, протянули ручки к знаниям. Хотя все «изучали» в школе физику, но по жизни простейшая задачка вызывает ступор. Наша цель — понять возможности перераспределения нагрузок на оси тягача и полуприцепа при изменении расположения груза в полуприцепе. И применение этого знания на практике.
Все уравнения, описывающие наши объекты, относятся к тем моментам, когда они либо находятся в состоянии покоя, либо двигаются равномерно и прямолинейно (с точки зрения классической механики эти состояния описываются одними и теми же уравнениями и, находясь внутри системы, невозможно понять, покоится ли она или двигается равномерно и прямолинейно). В эти моменты сумма всех сил, действующих на каждый из рассматриваемых объектов, равна нулю. А также сумма всех моментов сил, действующих на каждый из объектов, равна нулю.
Наша задача не привязана к какому-либо конкретному типу тягачей, полуприцепов и грузов. Поэтому все формулы будут предоставлены в общем виде. Однако, поскольку нашей целью не является получение абстрактных формул и решение систем уравнений, а мы хотим решить практические вопросы, то величины, которые могут быть измерены на практике, будут полагаться известными. Кроме того, мы будем рассматривать двуосный тягач и одноосный полуприцеп. В нулевом приближении при увеличении количества осей у тягача и/или полуприцепа нагрузка на каждую ось уменьшается пропорционально. Т.е. если мы получим, что нагрузка на одну ось составляет 10 тонн, то замена одной оси на 2 приведёт к тому, что нагрузка на каждую из осей будет составлять 5 тонн. Если практические измерения покажут неприменимость такого подхода, при котором нагрузка делится между осями поровну, то необходимо будет уточнить и дополнить модель.
Рассмотрение системы из 3-х объектов будем проводить последовательно, т.е. сначала рассмотрим один тягач, затем добавим к нему полуприцеп, после чего добавим груз и посмотрим, как можно оптимизировать нагрузку на оси тягача и полуприцепа, изменяя положение груза в полуприцепе.
1. Тягач
Любая задача в механике начинается с рисунка, на котором отмечены все важные в контексте задачи геометрические размеры; силы, действующие на объекты; а также указана система отсчета, в которой мы пишем все уравнения.
Рисунок 1.
Итак, условие, что сумма всех сил, действующих на тело равна нулю, приводит нас к уравнению:
Рассмотрим ось, проходящую через переднюю ось грузовика (и направленную, как мы договаривались ранее, перпендикулярно плоскости рисунка). Сумма всех моментов сил действующих на тело, равна $0$. Это следует из того, что раз грузовик находится в состоянии покоя (а он очевидно находится в состоянии покоя, см. также замечание относительно состояния покоя и равномерного прямолинейного движения во вступлении), то он не вращается вокруг любой выбранной оси. Значит он не вращается в том числе вокруг оси, проходящей через переднюю ось грузовика. Это даёт нам уравнение:
Как можно применить формулу (1.3) на практике?
Для этого рассмотрим тягач Mercedes Actros 1841.
Данные взяты не из бумажек, измерения проводились на реальном пункте взвешивания — на весах. В баке было 500 литров дизельного топлива.
Расстояние между осями нашего тягача Mercedes Actros 1841 — 3600 мм.
Чтобы корректно подставить эти значения в формулу (1.3) обсудим сначала вопрос о размерности физических величин.
Масса — скалярная величина, измеряется в килограммах. Сила — векторная величина, измеряется в Ньютонах.
Таким образом, мы видим, что сила однозначно связана с массой, и в принципе, нам всё равно, в чём измерять силу — в Ньютонах или в килограммах — это вопрос договорённости. Когда речь идёт о нагрузке, которую оказывает автомобиль на дорогу, общепринятой единицей измерения этой нагрузки являются килограммы. В формулу (1.3) входит отношение нагрузки на заднюю ось к весу тягача. Вес (по определению) это сила, с которой тело давит на горизонтальную опору или растягивает вертикальный подвес. Таким образом, вес — это сила. Но раз мы договорились о том, что все силы мы измеряем не в Ньютонах (как мы все привыкли со школы), а в килограммах, то и вес тягача мы выражаем в килограммах. Т.е. от веса переходим к массе.
Итак, давайте рассчитаем расстояние от передней оси тягача Mercedes Actros 1841 по формуле (1.3) с учётом рассуждений о единицах измерения:
Все рассуждения о нагрузке, которая измеряется в килограммах, будут применяться и в дальнейшем при практическом применении выведенных формул. См., например, вычисление центра тяжести полуприцепа по формуле (2.4).
2. Тягач с полуприцепом
Если к тягачу, рассмотренному ранее, присоединён полуприцеп без груза, то нагрузка на его оси изменяется.
Рисунок 2.
Рассмотрим рис.2. Мы можем записать по отдельности для тягача и полуприцепа оба условия равновесия. Необходимо отметить, что положение центра тяжести тягача, вычисленное согласно (1.3), не изменится после присоединения полуприцепа.
Что даёт нам уравнение (2.1) с практической точки зрения? Если мы, зная массу тягача, измерим нагрузку на его переднюю и заднюю оси при присоединении пустого полуприцепа, то используя уравнение (2.1) мы можем вычислить силу, с которой пустой полуприцеп «давит» на тягач:
Рассмотрим теперь полуприцеп.
Для того чтобы определить, где находится центр тяжести полуприцепа (это важно — мы ищем положение центра тяжести именно самого полуприцепа, а не системы «тягач+пустой полуприцеп»), запишем условие равенства моментов сил, действующих на полуприцеп, относительно оси, проходящей через заднюю ось полуприцепа:
Эта формула пригодится нам в дальнейшем при рассмотрении груза, находящегося в полуприцепе. Также мы можем вычислить нагрузку на ось полуприцепа (считаем что ось на полуприцепе одна) по следующей формуле:
Полуприцеп трёхосный, но в рамках оговоренной ранее методики мы считаем нагрузку на каждую ось одинаковой. Посмотрим, к каким результатам нас это приведёт. Рассчитаем по формуле (2.2) силу взаимодействия тягача и полуприцепа, сила с которой полуприцеп давит на «седло» тягача:
Подставим теперь полученную величину в формулы (2.4) и (2.5):
Если теперь мы хотим рассчитать нагрузку на каждую из осей, то общую нагрузку необходимо поделить на 3 (т.к. у полуприцепа 3 оси). Полученный результат можно показать при помощи следующей таблицы:
Отклонение расчёта от
реального значения, кг
3. Тягач с полуприцепом и грузом
Перейдём теперь к рассмотрению общего случая, когда в полуприцепе находится груз. Теперь мы должны на основании рассчитанных ранее характеристик грузовика и полуприцепа выяснить, как будут распределяться нагрузки на оси при различном положении груза. При этом необходимо сделать следующую оговорку: мы будем предполагать, что рама полуприцепа является идеально жесткой, не деформируется при наличии груза и распределяет нагрузку равномерно на каждый метр своей длины. Т.е. истории, подобные той, что описана на сайте в разделе страшных рассказов, выходят за рамки текущей задачи.
Рисунок 3.
Итак, запишем условие равенства сил, и моментов сил, действующих на тягач:
Теперь запишем аналогичную пару уравнений для полуприцепа, при этом условие равенства моментов сил будем рассматривать относительно задней оси полуприцепа.
Итак, запишем условие равенства сил, и моментов сил, действующих на тягач:
$ <\large m^
4. Что нужно для расчета нагрузок на оси грузового автопоезда
Итак, любая модель подразумевает в первую очередь набор исходных данных; переменную величину, изменяющееся значение которой влияет на результаты; алгоритм расчёта и результат.
Что нам необходимо в качестве исходных данных?
Нужно геометрическое описание тягача и полуприцепа:
| $<\large L_T>$ | — расстояние между осями тягача; |
| $<\large l_1>$ | — расстояние от передней оси тягача до точки сцепки с полуприцепом; |
| $<\large L^ | — расстояние от задней оси полуприцепа до места сцепки с тягачом. |
Необходимо знать распределение нагрузки на оси тягача без полуприцепа:
$<\large N_<1<,>0>^
$<\large N_<2<,>0>^
Необходимо знать распределение нагрузки на оси тягача при присоединении полуприцепа без груза:
$<\large N_<1<,>1>^
$<\large N_<2<,1>>^
Если каждый груз представляет из себя коробку, внутри которой вес распределен равномерно, то центр тяжести находится на середине ширины коробки. В данном случае шириной мы называем геометрический размер стороны коробки, параллельный борту полуприцепа.
Поупражняйтесь в расчетах и распределении груза
Мы сделали калькулятор для расчета нагрузок на оси грузового автопоезда в составе седельного тягача и полуприцепа.
5. О распределении нагрузки на задние оси полуприцепа
Ранее было сделано предположение о том, что нагрузка на задние оси полуприцепа распределяется равномерно. Это предположение приводит к расхождению теоретических расчётов с экспериментальными результатами. Причём пренебречь этими расхождениями мы не можем, поскольку они превышают точность измерений на статических весах в пунктах весового контроля.
Для учёта неравномерной нагрузки можно применить несколько различных подходов:
Ослабление исходной модели.
Давайте проверим, к чему нас это предположение приведёт. Уравнения (4.1), (4.2) принимают вид:
Методика расчета нагрузки на ось для грузовых автоперевозок
Тяга к знаниям — она как «старость», в самый неожиданный момент может настичь любого. Вот и мы, застигнутые врасплох, протянули ручки к знаниям. Хотя все «изучали» в школе физику, но по жизни простейшая задачка вызывает ступор. Наша цель — понять возможности перераспределения нагрузок на оси тягача и полуприцепа при изменении расположения груза в полуприцепе. И применение этого знания на практике.
Все уравнения, описывающие наши объекты, относятся к тем моментам, когда они либо находятся в состоянии покоя, либо двигаются равномерно и прямолинейно (с точки зрения классической механики эти состояния описываются одними и теми же уравнениями и, находясь внутри системы, невозможно понять, покоится ли она или двигается равномерно и прямолинейно). В эти моменты сумма всех сил, действующих на каждый из рассматриваемых объектов, равна нулю. А также сумма всех моментов сил, действующих на каждый из объектов, равна нулю.
Наша задача не привязана к какому-либо конкретному типу тягачей, полуприцепов и грузов. Поэтому все формулы будут предоставлены в общем виде. Однако, поскольку нашей целью не является получение абстрактных формул и решение систем уравнений, а мы хотим решить практические вопросы, то величины, которые могут быть измерены на практике, будут полагаться известными. Кроме того, мы будем рассматривать двуосный тягач и одноосный полуприцеп. В нулевом приближении при увеличении количества осей у тягача и/или полуприцепа нагрузка на каждую ось уменьшается пропорционально. Т.е. если мы получим, что нагрузка на одну ось составляет 10 тонн, то замена одной оси на 2 приведёт к тому, что нагрузка на каждую из осей будет составлять 5 тонн. Если практические измерения покажут неприменимость такого подхода, при котором нагрузка делится между осями поровну, то необходимо будет уточнить и дополнить модель.
Рассмотрение системы из 3-х объектов будем проводить последовательно, т.е. сначала рассмотрим один тягач, затем добавим к нему полуприцеп, после чего добавим груз и посмотрим, как можно оптимизировать нагрузку на оси тягача и полуприцепа, изменяя положение груза в полуприцепе.
1. Тягач
Любая задача в механике начинается с рисунка, на котором отмечены все важные в контексте задачи геометрические размеры; силы, действующие на объекты; а также указана система отсчета, в которой мы пишем все уравнения.
Рисунок 1.
Итак, условие, что сумма всех сил, действующих на тело равна нулю, приводит нас к уравнению:
Рассмотрим ось, проходящую через переднюю ось грузовика (и направленную, как мы договаривались ранее, перпендикулярно плоскости рисунка). Сумма всех моментов сил действующих на тело, равна $0$. Это следует из того, что раз грузовик находится в состоянии покоя (а он очевидно находится в состоянии покоя, см. также замечание относительно состояния покоя и равномерного прямолинейного движения во вступлении), то он не вращается вокруг любой выбранной оси. Значит он не вращается в том числе вокруг оси, проходящей через переднюю ось грузовика. Это даёт нам уравнение:
Как можно применить формулу (1.3) на практике?
Для этого рассмотрим тягач Mercedes Actros 1841.
Данные взяты не из бумажек, измерения проводились на реальном пункте взвешивания — на весах. В баке было 500 литров дизельного топлива.
Расстояние между осями нашего тягача Mercedes Actros 1841 — 3600 мм.
Чтобы корректно подставить эти значения в формулу (1.3) обсудим сначала вопрос о размерности физических величин.
Масса — скалярная величина, измеряется в килограммах. Сила — векторная величина, измеряется в Ньютонах.
Таким образом, мы видим, что сила однозначно связана с массой, и в принципе, нам всё равно, в чём измерять силу — в Ньютонах или в килограммах — это вопрос договорённости. Когда речь идёт о нагрузке, которую оказывает автомобиль на дорогу, общепринятой единицей измерения этой нагрузки являются килограммы. В формулу (1.3) входит отношение нагрузки на заднюю ось к весу тягача. Вес (по определению) это сила, с которой тело давит на горизонтальную опору или растягивает вертикальный подвес. Таким образом, вес — это сила. Но раз мы договорились о том, что все силы мы измеряем не в Ньютонах (как мы все привыкли со школы), а в килограммах, то и вес тягача мы выражаем в килограммах. Т.е. от веса переходим к массе.
Итак, давайте рассчитаем расстояние от передней оси тягача Mercedes Actros 1841 по формуле (1.3) с учётом рассуждений о единицах измерения:
Все рассуждения о нагрузке, которая измеряется в килограммах, будут применяться и в дальнейшем при практическом применении выведенных формул. См., например, вычисление центра тяжести полуприцепа по формуле (2.4).
2. Тягач с полуприцепом
Если к тягачу, рассмотренному ранее, присоединён полуприцеп без груза, то нагрузка на его оси изменяется.
Рисунок 2.
Рассмотрим рис.2. Мы можем записать по отдельности для тягача и полуприцепа оба условия равновесия. Необходимо отметить, что положение центра тяжести тягача, вычисленное согласно (1.3), не изменится после присоединения полуприцепа.
Что даёт нам уравнение (2.1) с практической точки зрения? Если мы, зная массу тягача, измерим нагрузку на его переднюю и заднюю оси при присоединении пустого полуприцепа, то используя уравнение (2.1) мы можем вычислить силу, с которой пустой полуприцеп «давит» на тягач:
Рассмотрим теперь полуприцеп.
Для того чтобы определить, где находится центр тяжести полуприцепа (это важно — мы ищем положение центра тяжести именно самого полуприцепа, а не системы «тягач+пустой полуприцеп»), запишем условие равенства моментов сил, действующих на полуприцеп, относительно оси, проходящей через заднюю ось полуприцепа:
Эта формула пригодится нам в дальнейшем при рассмотрении груза, находящегося в полуприцепе. Также мы можем вычислить нагрузку на ось полуприцепа (считаем что ось на полуприцепе одна) по следующей формуле:
Полуприцеп трёхосный, но в рамках оговоренной ранее методики мы считаем нагрузку на каждую ось одинаковой. Посмотрим, к каким результатам нас это приведёт. Рассчитаем по формуле (2.2) силу взаимодействия тягача и полуприцепа, сила с которой полуприцеп давит на «седло» тягача:
Подставим теперь полученную величину в формулы (2.4) и (2.5):
Если теперь мы хотим рассчитать нагрузку на каждую из осей, то общую нагрузку необходимо поделить на 3 (т.к. у полуприцепа 3 оси). Полученный результат можно показать при помощи следующей таблицы:
Отклонение расчёта от
реального значения, кг
3. Тягач с полуприцепом и грузом
Перейдём теперь к рассмотрению общего случая, когда в полуприцепе находится груз. Теперь мы должны на основании рассчитанных ранее характеристик грузовика и полуприцепа выяснить, как будут распределяться нагрузки на оси при различном положении груза. При этом необходимо сделать следующую оговорку: мы будем предполагать, что рама полуприцепа является идеально жесткой, не деформируется при наличии груза и распределяет нагрузку равномерно на каждый метр своей длины. Т.е. истории, подобные той, что описана на сайте в разделе страшных рассказов, выходят за рамки текущей задачи.
Рисунок 3.
Итак, запишем условие равенства сил, и моментов сил, действующих на тягач:
Теперь запишем аналогичную пару уравнений для полуприцепа, при этом условие равенства моментов сил будем рассматривать относительно задней оси полуприцепа.
Итак, запишем условие равенства сил, и моментов сил, действующих на тягач:
$ <\large m^
4. Что нужно для расчета нагрузок на оси грузового автопоезда
Итак, любая модель подразумевает в первую очередь набор исходных данных; переменную величину, изменяющееся значение которой влияет на результаты; алгоритм расчёта и результат.
Что нам необходимо в качестве исходных данных?
Нужно геометрическое описание тягача и полуприцепа:
| $<\large L_T>$ | — расстояние между осями тягача; |
| $<\large l_1>$ | — расстояние от передней оси тягача до точки сцепки с полуприцепом; |
| $<\large L^ | — расстояние от задней оси полуприцепа до места сцепки с тягачом. |
Необходимо знать распределение нагрузки на оси тягача без полуприцепа:
$<\large N_<1<,>0>^
$<\large N_<2<,>0>^
Необходимо знать распределение нагрузки на оси тягача при присоединении полуприцепа без груза:
$<\large N_<1<,>1>^
$<\large N_<2<,1>>^
Если каждый груз представляет из себя коробку, внутри которой вес распределен равномерно, то центр тяжести находится на середине ширины коробки. В данном случае шириной мы называем геометрический размер стороны коробки, параллельный борту полуприцепа.
Поупражняйтесь в расчетах и распределении груза
Мы сделали калькулятор для расчета нагрузок на оси грузового автопоезда в составе седельного тягача и полуприцепа.
5. О распределении нагрузки на задние оси полуприцепа
Ранее было сделано предположение о том, что нагрузка на задние оси полуприцепа распределяется равномерно. Это предположение приводит к расхождению теоретических расчётов с экспериментальными результатами. Причём пренебречь этими расхождениями мы не можем, поскольку они превышают точность измерений на статических весах в пунктах весового контроля.
Для учёта неравномерной нагрузки можно применить несколько различных подходов:
Ослабление исходной модели.
Давайте проверим, к чему нас это предположение приведёт. Уравнения (4.1), (4.2) принимают вид: