расчет пространственной рамы автомобиля

Содержание

9.2. Расчет рамы автомобиля

Рама автомобиля представляет собой пространственную несущую систему, нагруженную статическими и динамическими нагрузками. Напряжения в элементах рамы определяются: изгибом в вертикальной плоскости под влиянием симметричной системы сил; кручением вокруг продольной оси под влиянием кососимметричной системы сил; изгибом в горизонтальной плоскости; местными нагрузками (подвеска топливного бака, запасного колеса, усилия при буксировке и др.).

Статические нагрузки возникают под действием собственного веса рамы и веса механизмов, кузова и полезного груза и от реакций опор рессор. Уже после сборки автомобиля в его раме возникают напряжения изгиба, составляющие 10  15% предела текучести материала. При этом напряжения в лонжеронах в 2  2,5 раза превышают напряжения в поперечинах.

При движении автомобиля на раму действуют динамические нагрузки. Основной причиной возникновения симметричных динамических нагрузок являются силы инерции подрессоренных масс, действующие на раму при колебаниях автомобиля. Вертикальные и угловые колебания автомобиля в вертикальной плоскости обусловлены симметричными составляющими прогибов подвески. Эти колебания вызывают изгиб рамы, создавая напряжения в лонжеронах и незначительные напряжения в поперечинах.

Изгибающая динамическая нагрузка зависти от статической нагрузки и вертикальных ускорений в точках приложения вертикальной нагрузки:

. (9.1)

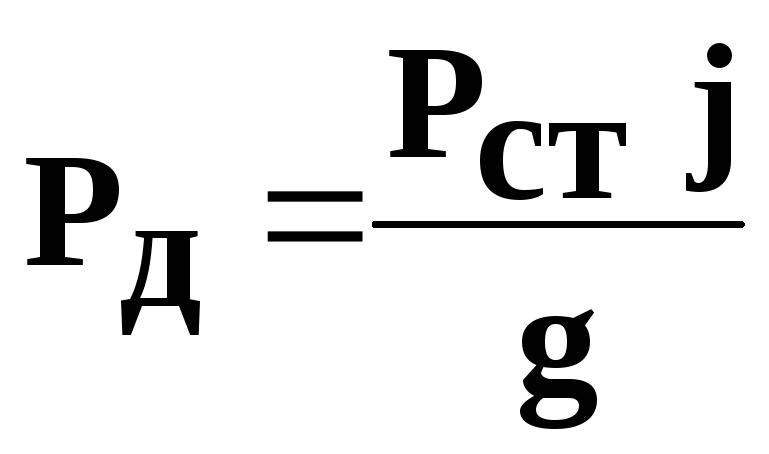
Динамические нагрузки существенно превышают статические и определяются с помощью коэффициента динамичности:

. (9.2)

Кососимметричные составляющие прогибов подвески вызывают бортовую качку и кручение рамы, создавая напряжения в поперечинах.

При кручении рамы возникают горизонтальные составляющие нагрузок. Они зависят от боковой жесткости рессор и смещения оси вращения от плоскости рамы, а также от угла закручивания. Чем больше жесткость рессор, смещение оси вращения и угол закручивания, тем больше горизонтальные усилия. Таким образом, элементы рамы при перекосе находятся в сложном нагружении под действием вертикального изгиба, стесненного кручения, горизонтального изгиба и др.

Для расчета рамы обычно рассматривают два режима:

движение с большой скоростью по дороге с мелкими неровностями (симметричное нагружение);

преодоление больших неровностей с вывешиванием некоторых колес (кососимметричное нагружение).

Для того чтобы не только оценить общую податливость рамы и действующие в ней напряжения, но и выявить опасные места резкого изменения деформаций и напряжений и темп их изменения по длине рамы, значения прогибов, углов закручивания и напряжений следует рассчитывать для ряда поперечных плоскостей, проходящих через характерные точки (места присоединения поперечин, изменения высоты или ширины сечения лонжерона, приложения нагрузок и т.д.). Результаты расчета целесообразно представлять в виде эпюр прогибов, углов закручивания и напряжений по длине рамы.

Расчет на симметричное нагружение (изгиб) простейшей лестничной рамы заключается в определении прогибов и напряжений в лонжеронах, представленных в виде элементарной балки на опорах.

Напряжение изгиба в каждом расчетном сечении лонжерона определяют по формуле:

, (9.3)

где – изгибающий момент.

Изгибающий момент в расчетном сечении лонжерона рассчитывают по формуле:

, (9.4)

где и– изгибающий момент и перерезывающая сила в предыдущем сечении, значения которых уже известны;– расстояние между сечениями.

Допускаемые напряжения при кратковременных динамических нагрузках можно приближенно определить как

, (9.5)

где – предел текучести материала лонжерона.

При расчете на кососимметричное нагружение (кручение) рама, состоящая из двух лонжеронов, связанных несколькими поперечинами, будет представлять собой статически неопределимую систему. Силовые факторы, действующие в элементах статически неопределимой системы (и углы закручивания), могут быть определены различными методами, излагаемыми в курсах сопротивления материалов, которые связаны с громоздкими и трудоемкими вычислениями. Однако при некоторых допущениях расчет может быть значительно упрощен. Если предположить, что деформации изгиба в элементах рамы малы по сравнению с деформациями кручения, то можно воспользоваться следующим приближенным методом.

При расчете на кручение рама рассматривается как плоская система, состоящая из прямолинейных тонкостенных стержней. Так как жесткость на изгиб у лонжеронов в сотни раз больше их жесткости на кручение, деформациями изгиба пренебрегают.

При прогибе поперечные сечения стержней остаются плоскими, а при кручении они искривляются (депланируют). Искривление сечений по длине стержня неодинаково. В узлах, усиленных косынками и приклепанных к полкам лонжеронов, искривление считают равным нулю, а в остальных сечениях оно может быть существенным. Такой характер деформации называется стесненным кручением.

При стесненном кручении кроме касательных напряжений кручения в сечениях лонжеронов из-за искривления появляются дополнительные нормальные напряжения.

В поперечинах рамы дополнительных нормальных напряжений не возникает из-за их более эластичного крепления к стенкам лонжеронов. Поэтому считают, что поперечины рамы испытывают свободное кручение.

Разрезав поперечины в плоскости симметрии рамы и приложив в местах разреза внутренние крутящие моменты и перерезывающие силы переходят от статически неопределимой системы к статически определимой, которую и принимают за расчетную схему (б). Строят эпюры изгибающих моментов (в) и бимоментов (г). По этим двум эпюрам определяют суммарные напряжения и строят их эпюру (д).

Момент, закручивающий раму, зависит от большого количества факторов, и может быть определен по формуле:

, (9.6)

где – высота преодолеваемых автомобилем неровностей;– колея колес;– угловая жесткость рамы;– угловая жесткость подвески.

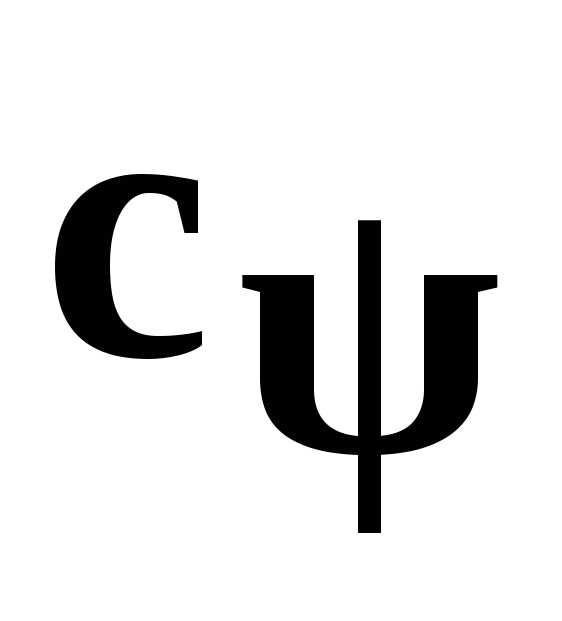
Из формулы (9.6) следует, что чем меньше угловая жесткость рамы, тем меньше закручивающий момент и, следовательно, выше прочность рамы. Кроме того, более эластичная рама вместе с подвеской обеспечивает лучшую приспособляемость колесам автомобиля к дорожным неровностям и постоянный контакт колес с дорогой. Однако при слишком эластичной раме возможно нарушение взаимного положения и условий работы агрегатов и механизмов, установленных на раме. Оптимальная жесткость рамы на кручение окончательно определяется и выбирается при доводочных испытаниях.

Суммарные нормальные напряжения в сечениях лонжеронов при стесненном кручении рассчитывают по формуле:

, (9.7)

где и– изгибающий момент и момент сопротивления сечения изгибу;– биомомент;– секториальный момент сопротивления сечения.

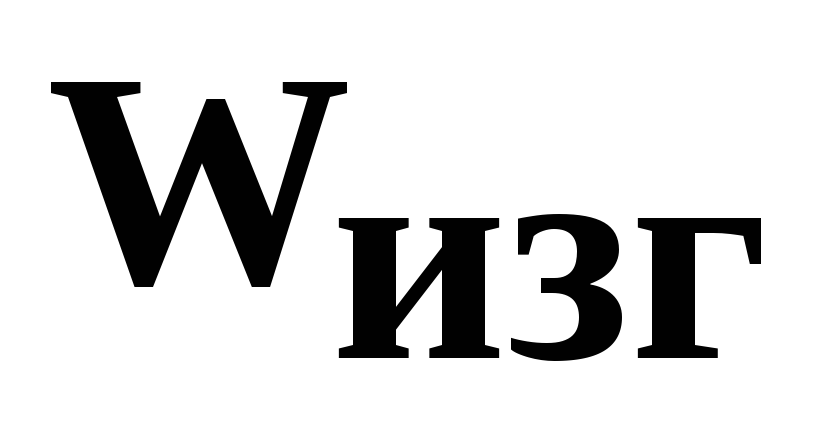
Биомомент для наиболее распространенного швеллерного сечения лонжеронов определяют по формуле:

, (9.8)

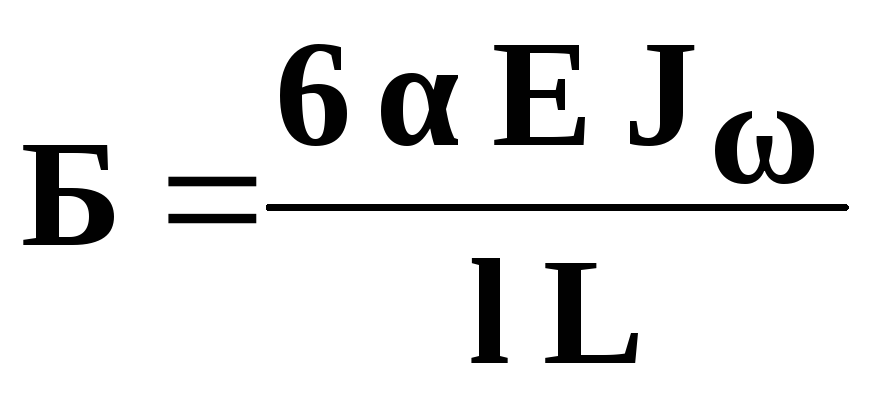
где –угол закручивания рамы на длине базы автомобиля; –модуль упругости 1-го рода; – секториальный момент инерции сечения; – длина рассматриваемого отрезка лонжерона; – база автомобиля.

Результирующие касательные напряжения кручения при деформации лонжеронов рамы в общем случае складываются из касательных напряжений свободного кручения, касательных напряжений изгиба и касательных напряжений стесненного кручения.

Наиболее значительными из них являются касательные напряжения свободного кручения, которые составляют 85  90% от результирующих напряжений.

Для лонжеронов, имеющих швеллерное сечение, касательные напряжения свободного кручения определяют по формуле:

, (9.9)

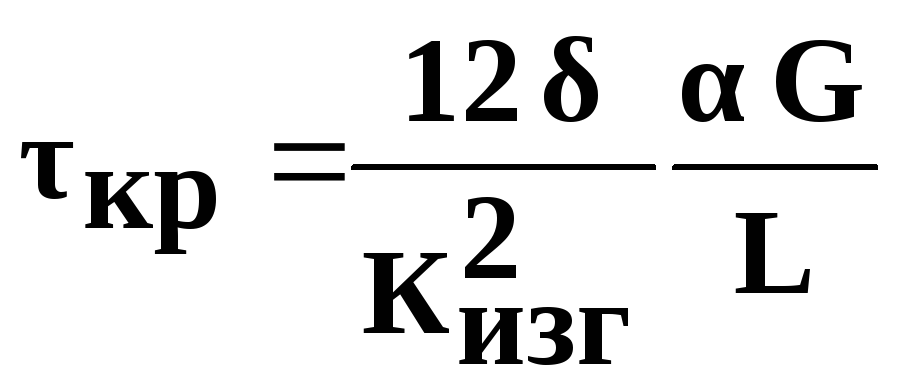
где – толщина профиля лонжерона; – модуль упругости 2-го рода; – изгибно-крутильная характеристика поперечного сечения лонжерона.

Напряжения для рам грузовых автомобилей, имеющих швеллерное сечение, при закручивании на угол = 10  12° составляют = 5  20 МПа (меньшие значения для лонжеронов, большие – для поперечин), а суммарные нормальные напряжения = 100  300 МПа.

Во время движения автомобиля по неровной дороге при максимальном закручивании рамы напряжения в ее элементах в 3  5 раз больше напряжений, возникающих после установки на раме кузова, агрегатов и механизмов.

В рамах грузовых автомобилей с обычной грузовой платформой наибольшие напряжения в лонжеронах возникают в зоне третьей поперечины, примерно у переднего борта кузова. У седельных тягачей наибольшие напряжения в лонжеронах возникают в зоне пятой поперечины у кронштейнов подвески. Из поперечин наиболее нагруженной обычно является первая поперечина.

Слабыми местами рамы являются зоны присоединения к лонжеронам поперечин, кронштейнов и других деталей.

Заклепочные соединения работают при стесненном кручении и горизонтальном изгибе. Независимо от технологии клепки заклепки разрушаются от изгиба.

В предельном случае можно рассматривать изгиб стержня заклепки в условиях, когда стенки отверстия не препятствуют деформации изгиба под действием изгибающего момента

, (9.10)

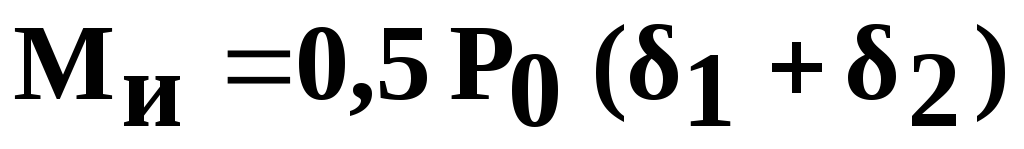
где –усилие, создающее изгибающий момент; , – толщины соединяемых деталей.

Напряжение изгиба у головки заклепки рассчитывают по формуле:

, (9.11)

где d – диаметр заклепки.

Напряжение среза (оно почти в 2 раза меньше напряжения изгиба) определяют по формуле:

, (9.12)

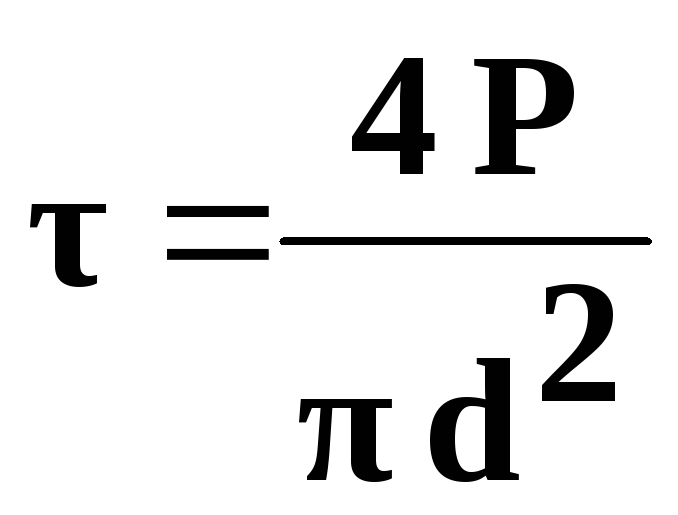
где – усилие, создающее напряжение среза.

Источник

Общие принципы расчёта кузова (рамы) на работоспособность.

При движении автомобиля несущий кузов воспринимает изгибающие нагрузки от веса груза, пассажиров, установленных на нем агрегатов и механизмов, а также от собственного веса. Кузов воспринимает также крутящие нагрузки при боковых кренах и перекосах мостов, инерционные нагрузки при разгоне и торможении, испытывает вибрации при собственных колебаниях.

Кузов представляет собой пространственную систему, и его расчет на сложные напряжения изгиба и кручения весьма затруднителен.

Расчет кузова производится различными приближенными методами с упрощениями и допущениями. К этим методам относятся следующие: метод потенциальной энергии, метод тонкостенных стержней и метод конечных элементов.

Метод потенциальной энергии используют при сравнительных расчетах на начальной стадии проектирования кузова.

Метод, основанный на теории тонкостенных стержней, применяют после завершения разработки конструкции кузова.

Метод конечных элементов является наиболее точным при расчете кузова. Этот метод основан на совместном рассмотрении напряженного состояния системы небольших элементов конечного размера. Метод заключается в том, что реальная конструкция кузова автомобиля заменяется структурной моделью (рис 14.18), состоящей из простейших элементов (стержни, пластины и другие объемные детали) с известными упругими свойствами. А при известных упругих свойствах отдельных элементов можно определить свойство кузова при определенных нагрузках.

Расчет кузова выполняют за несколько этапов. Вначале кузов разбивают на отдельные простые элементы. При этом на одной половине по оси симметрии кузов разбивают на 200 — 500 элементов. Затем получают координаты узловых точек кузова. После этого проводят расчет с использованием ЭВМ.

Однако основным методом оценки прочности кузова являются стендовые или дорожные испытания кузова на изгиб и кручение.

Прочность кузова оценивают по пределу текучести материала as. При одностороннем растяжении или сжатии допускаемые напряжения

где £без = 1,3. 1,8 — коэффициент безопасности, учитывающий местные концентраторы напряжений, технологические отступления, нестабильность механических свойств и др.

Удельная крутильная жесткость кузова характеризует сопротивление кузова закручиванию. Она представляет

собой отношение крутящего момента к углу закручивания кузова на длине базы автомобиля, умноженное на размер базы. Для легковых автомобилей удельная крутящая жесткость кузова составляет 130. 300 Н*м2/°.

Удельная изгибная жесткость кузова характеризует изгиб кузова в вертикальной плоскости. Она представляет собой отношение нагрузки к прогибу кузова, умноженному на размер базы автомобиля в третьей степени. Для легковых автомобилей изгибная жесткость кузова находится в пределах 850. 2 200 Н • м2/°.

Для изготовления автомобильных кузовов применяют стали, физико-механические свойства которых позволяют в высокой степени механизировать и автоматизировать производство кузовов.

В связи с высокими требованиями к штампуемое для кузовов используют низкоуглеродистую сталь 08кп и конструкционную сталь 08.

Для панелей большого размера (крыша, задние крылья, двери, пол и др.) применяют листовую сталь толщиной 0,9 и 0,75 мм. Детали каркаса (стойки, пороги, продольные балки и поперечины основания) изготавливают из листов толщиной 1,0 и 1,3 мм. Для отдельных усилителей используют листы толщиной 1,6. 2,4 мм.

Нахождение центра тяжести.

Центр тяжести (ЦТ) машины определяется графически. Для этого на бумаге в клетку или миллиметровке в избранном масштабе вычерчивается схема автомобиля, на которой прорисовывается компоновка и наносятся точки, соответствующие центрам тяжести всех основных узлов (рис. 1).

Если отдельные элементы размещены несимметрично относительно продольной оси, необходимо выполнить в том же масштабе вторую проекцию.

Координата ЦТ машины определяется из общей суммы произведений веса каждого узла на собственную координату, деленной на полный вес автомобиля. Для нашего случая:

Из схемы и соответствующей ей таблицы нетрудно определить распределение нагрузки по осям, исходя из условия, что сумма моментов сил относительно любой из осей должна быть равна нулю. Так, относительно задней оси:

Σ Gi*(Х02- ХЦТ ) = G01 * (Х02-Х01),

Соответственно, нагрузка на заднюю ось составит: G02 = ΣGi-G01= 602-218 = 384 (кгс).

Источник

Расчёт рамы.

Строго говоря, рама автомобиля представляет собой сложную систему, так как часть нагрузки приложена не в продольных плоскостях, проходящих через точки опор. Однако, учитывая относительно небольшие нагрузки и расстояния между точками приложения сил и опорой, раму рассчитывают как обычную двухопорную балку.

В принятой схеме расчёта, нагрузки считают действующими в вертикальной плоскости. В систему сил включаются:

Опорами являются места установки колёс.

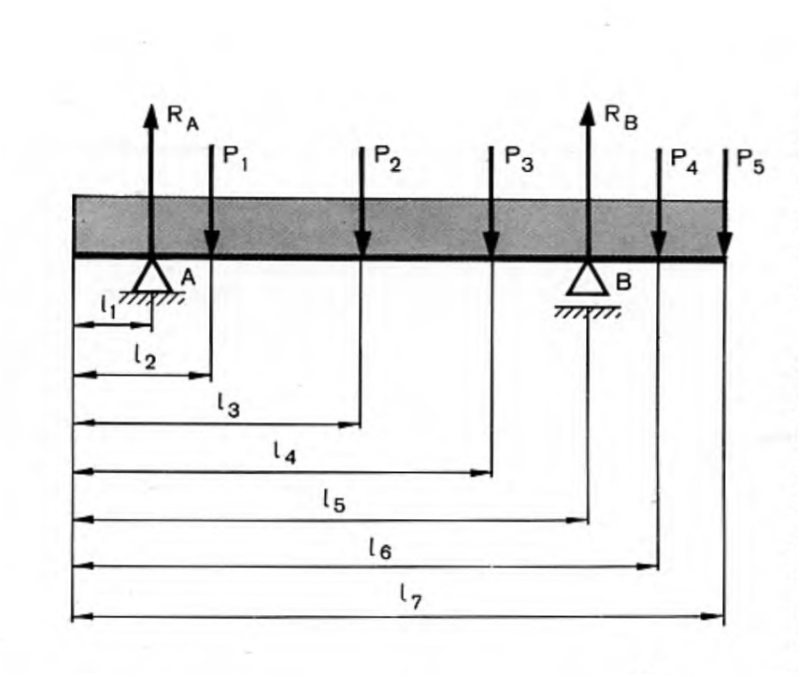
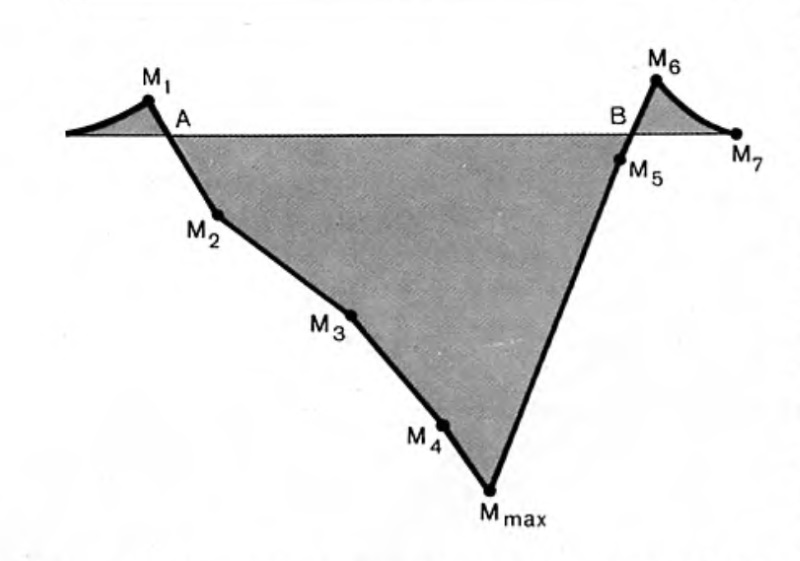
Обозначив действующие нагрузки через Р₁, Р₂, Р₃, Р₄, Р₅ (рис), распределённую нагрузку — через ql, расстояния до точек приложения нагрузок через l₁, l₂, l₃…,l₇, из условия равенства нулю моментов внешних сил определяют реакции в опорах R_A и R_B.

Для условия ?M_A= 0 (где M_A – момент сил относительно точки А)

Для условия ?M_B= 0 (где M_B – момент сил относительно точки B)

После определения реакций R_A и R_B в опорах проверяют выполнение условия равенства нулю суммы всех действующих сил в проекции на ось ординат

Затем рассчитывают изгибающие моменты в сечениях:

где силы – в Н, длинна отрезков – в см.

По вычисленным значениям изгибающих моментов строят эпюру.

Затем проводят анализ этой эпюры для определения максимального изгибающего момента M_MAX, для чего вводят текущую координату Х, считая, что в начале рамы Х = 0.

Определив максимальный изгибающий момент и задаваясь допускаемым напряжением (в Па), определяют необходимый момент сопротивления профиля лонжеронов с учетом того, что в работе участвуют два лонжерона и допущения, что на каждый из них действует одинаковая нагрузка:

где W_X_—_X – момент сопротивления профиля лонжерона, [?] – допускаемое напряжение при растяжении, Па.

По справочным данным выбирают необходимое сечение. В случаях, когда используется уже имеющийся профиль, проверяют его на прочность из условия, что:

Если напряжение в точке максимального изгибающего момента превышает допустимое значение, то обычно усиливают лонжероны, применяя накладки, и повторно рассчитывают момент сопротивления этого соединения.

При самостоятельном изготовлении автомобиля обычно применяют еще и каркас для крепления кузова, который также воспринимает нагрузки. В связи с тем, что каркас повышает прочность кузова, его в расчёте не учитывают.

Приведённый расчёт рамы является приблизительным. С учётом коэффициента понижения допускаемых напряжений, равно 1,5. Можно использовать его с уверенностью, что рама будет надёжной в эксплуатации.

Данная статья была подготовлена по материалам книги «Я строю автомобиль» В. Захарченко и И. Туревский изд. «Машиностроение» 1989 г.

Источник