14.3. Расчет тормозных механизмов
Целью проектного расчета тормозных механизмов является выбор основных их конструктивных параметров и приводной силы, необходимых для получения требуемого тормозного момента. Определение этих параметров осуществляется исходя их нормативов эффективности тормозных систем.
Расчет барабанных тормозных механизмов рабочей тормозной системы рекомендуется проводить в следующем порядке.
1. По заданной интенсивности торможения определяют суммарный тормозной момент на мостах автомобиля. Применительно к двухосному автомобилю:
, (14.13)
где 
– расчетное замедление автомобиля при торможении.
Максимальную тормозную силу можно получить, когда сцепная масса автомобиля используется полностью. При этом тормозные силы должны быть пропорциональны нормальным реакциям на колесах:
, (14.14)
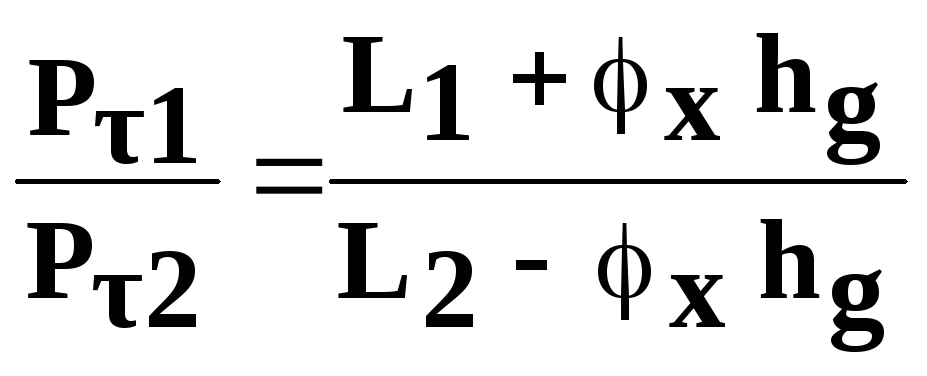
где 
и
– расстояния от центра масс автомобиля до передней и задней оси соответственно;
– высота центра масс;
– продольный коэффициент сцепления.
2. Выбирают тип тормозного механизма; задаются его основными размерами (
, a, c, e); требуемые значения 
и
находят по вышеприведенным формулам с учетом того, что радиус барабана обуславливается необходимостью размещения его в колесе автомобиля. Как правило, в выполненных конструкциях, он принят на 20 ÷ 30 мм меньше внутреннего радиуса обода колеса;a = c = 0,8
, e = 0,85
.
3. Ширину фрикционных накладок b рассчитывают, исходя из допустимого давления между барабаном и колодкой, определяемого по формуле:
, (14.15)
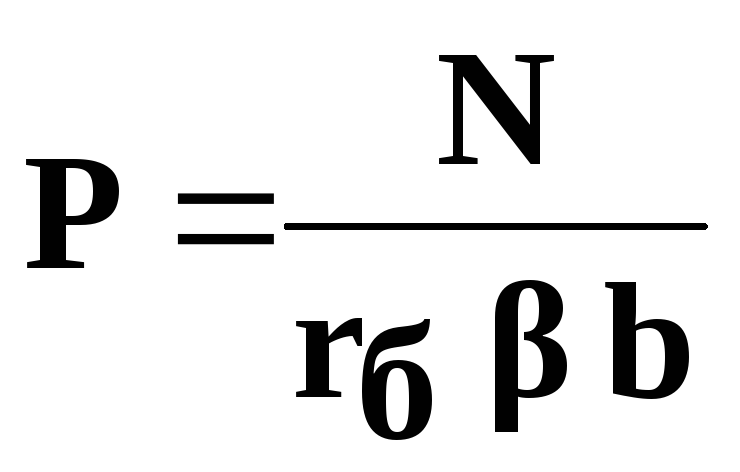
где 
– угол обхвата колодки.
Допустимое давление – [
] = 2 МПа.
4. Производят расчет тормозного механизма на энергонапряженность. Срок службы накладок зависит не только от давления между ними и барабаном, но и от удельной работы трения, которую рассчитывают по формуле:
, (14.16)
где 
– кинетическая энергия автомобиля;
– суммарная площадь всех фрикционных накладок.
От удельной работы зависит износ и нагрев элементов тормозного механизма: тормозного барабана (диска), тормозных накладок. Для уменьшения удельной работы необходимо увеличивать площадь тормозных накладок и соответственно ширину тормозных барабанов и их диаметр.
При этом увеличение поверхности охлаждения благоприятно сказывается на режиме торможения. Этим объясняется наблюдаемая в последнее время тенденция увеличения размера колес легковых автомобилей для возможности размещения тормозных барабанов увеличенных размеров.
Нагрев тормозного барабана (диска) за одно торможение определяют по формуле:
, (14.17)
где 
–масса автомобиля, приходящаяся на тормозящее колесо; 
– начальная скорость торможения; 
– масса барабана (диска); 
– удельная теплоемкость материала барабана (диска).
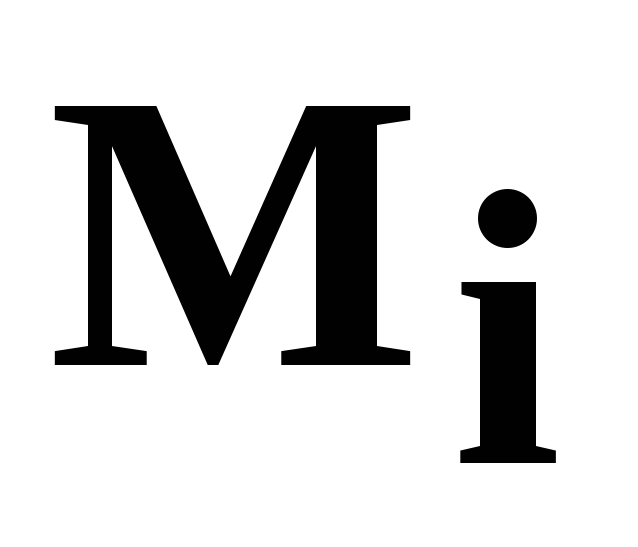
Допустимый нагрев барабана (диска) за одно торможение – [
] = 20° С.
Болты крепления барабана рассчитываются на срез. Допустимые напряжения – [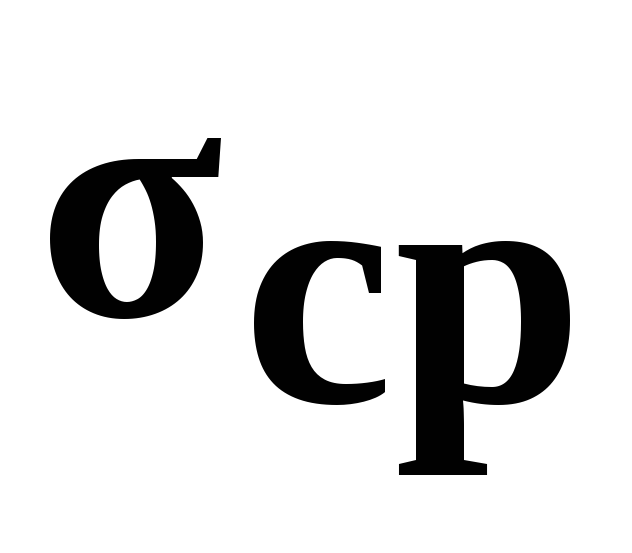
] = 110 МПа.
Вал разжимного кулака рассчитывается на кручение. Допустимые напряжения – [
] = 130 МПа.
Ряд деталей тормозов (разжимной кулак, нижние и верхние опоры и концы колодок) рассчитываются на смятие. Допустимые напряжения смятия в зависимости от материала деталей – [
] = 110 ÷ 230 МПа.
Расчёт тормозной системы автомобиля
Представлен расчёт тормозной системы и процесса торможения легкового автомобиля. На основе заданных параметров автомобиля и его тормозной системы находятся характеристики торможения.
Содержание
Привод тормозов [ править ]
В приводе тормозов усилие, прикладываемое к педали тормоза, преобразуется в давление в гидроприводе, которое, затем передаётся тормозным механизмам.
Привод без усилителя [ править ]
В приводе без усилителя, сила на педали тормоза F d <\displaystyle F_
непосредственно преобразуется в давление p m <\displaystyle p_на выходе главного тормозного цилиндра (ГТЦ)
Характеристика привода без усилителя описывается следующим уравнением:
Вакуумный усилитель [ править ]
В вакуумном усилителе тормозов к усилию на входе добавляется дополнительная сила, создаваемая за счёт разности давления в вакуумной и атмосферной полостях усилителя.
В реальном усилителе имеется сила сопротивления F s 0 <\displaystyle F_, вызванная противодействием пружин и сил трения. Кроме того, имеется скачок F s j <\displaystyle F_на характеристике, обусловленный конструктивными особенностями усилителя. С учетом всего этого, уравнение (4) запишется несколько иначе
Это соотношение действительно до тех пор, пока давление в атмосферной полости усилителя не станет равным атмосферному. Тогда, клапаны внутри усилителя полностью открываются, его следящее действие прекращается, происходит, так называемое, насыщение усилителя и к усилию на входе просто добавляется сила от разницы давлений в камерах.
Усилие на входе F s m a x <\displaystyle F_, при котором происходит насыщение усилителя, находится подстановкой в уравнение (6) значения усилия на выходе из уравнения (7).
Полностью характеристика вакуумного усилителя тормозов опишется следующим уравнением
Привод с усилителем [ править ]
В приводе с усилителем на вход усилителя тормозов подается сила от педали тормоза
а на выходе усилителя расположен главный тормозной цилиндр
Тогда, на с учётом зависимости (9), характеристика тормозного привода с усилителем описывается следующим уравнением
Если необходимо найти зависимость усилия на педали от давления в главном тормозном цилиндре, то такое уравнение запишется следующим образом
p_p_
Тормозные механизмы [ править ]
Тормозные механизмы (тормоза) преобразуют поступающее к ним из гидропривода давление в тормозной момент.
Барабанный тормоз [ править ]
Тормозной момент M b <\displaystyle M_> одной колодки барабанного тормоза находится как произведение равнодействующей F t <\displaystyle F_распределённых сил трения на условный радиус трения R 0 <\displaystyle R_<0>>
Тогда, тормозной момент колодки можно выразить следующим уравнением
Теперь, если из условия равновесия колодки относительно точки опоры (см. Рисунок 4), выразить равнодействующую сил давления, то тормозной момент колодки найдётся как
Для второй, пассивной или ведомой, колодки барабанного тормоза, расположенной симметрично, направление равнодействующей силы трения изменится на противоположное и её передаточное число C I I <\displaystyle C_будет равно
Коэффициент касательных сил для колодки со скользящей нижней опорой и синусоидальном распределении давления по длине контакта [2]
Тогда, в окончательном виде, тормозной момент барабанного тормоза находится как
Дисковый тормоз [ править ]
Расчёт дискового тормозного механизма аналогичен расчёту барабанного.
Поршень дискового тормоза напрямую прижимает колодку к диску, поэтому, сила прижатия колодки равна силе от привода
тогда передаточное число одной колодки, то есть отношение силы привода к тормозной силе будет просто равно коэффициенту трения
Радиус трения находится как центр тяжести кольцевого сектора
В итоге, тормозной момент дискового тормоза будет выражаться таким же, как и для барабанного уравнением
где передаточное число всего тормозного механизма с двумя колодками равно
Для обоих типов механизмов тормозной момент можно записать сокращённо
M b = k b ( p − p 0 ) ( 35 ) <\displaystyle M_=k_\ (p-p_<0>)\,\qquad (35)>
Торможение автомобиля [ править ]
Торможение до блокировки колёс [ править ]
При торможении автомобиля, из равенства действующих на него горизонтальных сил (см. Рисунок 6), замедление J a <\displaystyle J_> найдётся как
Тормозные силы на осях определяются тормозными моментами M b f <\displaystyle M_, M b r <\displaystyle M_
> , создаваемыми передними и задними тормозами
С учетом ранее выведенной формулы тормозного момента (35), эти уравнения можно записать по-другому
Отсюда нетрудно вычислить давления в передних и задних тормозах
Если давление в тормозных механизмах равно давлению в главном тормозном цилиндре, то есть,
то, после не сложных преобразований, зависимость замедления автомобиля от давления в приводе можно записать как
Теперь, если подставить в это уравнение ранее установленную взаимосвязь усилия на педали тормоза и давления в главном тормозном цилиндре (12), то можно построить зависимость замедления автомобиля от усилия на педали тормоза. Это то, что ощущает водитель при торможении, эргономическая характеристика тормозной системы, первая из важнейших характеристик тормозов.
Если необходимо найти давление в главном тормозном цилиндре по заданному замедлению, то его можно вычислить по следующей формуле
Предельные по сцеплению тормозные силы [ править ]
Рост тормозных сил на осях автомобиля не бесконечен. В определённый момент они достигают предельных величин, ограниченных сцеплением шин с дорогой. При этом, либо колёса блокируются, либо срабатывает автоблокировочная система тормозов (АБС). И в том, и в другом случае тормозные силы становятся равными предельным по сцеплению.
Вертикальные силы не сложно найти из уравнений моментов сил относительно точек контакта сначала передней, а затем задней осей (см. Рисунок 6)
Тогда, предельные по сцеплению тормозные силы на осях найдутся как
Торможение с заблокированными колёсами [ править ]
Если вспомнить, что давления в приводе тормозов каждой из осей равны (44) и, приравняв выраженные через давления значения тормозных сил (42) и (43), можно получить зависимость задней тормозной силы от передней.
Тогда, с учётом полученной зависимости и уравнения предельной по сцеплению тормозной силы (51), замедление автомобиля, при котором блокируется передняя ось J a f m a x <\displaystyle J_в соответствии с (37) будет равно
После этого, автомобиль будет тормозить со следующим замедлением
Если первыми блокируются колёса задней оси, то, на основе аналогичных рассуждений, замедление автомобиля при блокировке задней оси J a r m a x <\displaystyle J_будет следующим
но с другими коэффициентами
Далее, автомобиль будет тормозить со следующим замедлением
Следует заметить, что блокируется только одна ось автомобиля, та, у которой замедление блокировки меньше. После, некоторое время происходит торможение с соответствующим замедлением, а затем блокируется вторая ось (см. Рисунок 7). С этого момента автомобиль тормозит с максимальным, определяемым только сцеплением шин с дорогой замедлением J a m a x <\displaystyle J_равным
Тормозные силы [ править ]
Баланс тормозных сил [ править ]
При торможении автомобиля с максимально возможным замедлением, предельные по сцеплению тормозные силы будут равны
По этим зависимостям можно построить график соотношения (баланса) предельных по сцеплению тормозных сил, задавая изменение коэффициента сцепления. Точки на полученной кривой соответствуют его определённым значениям. Прямая на этом же графике показывает соотношение реальных тормозных сил на осях автомобиля.
Взаимное расположение двух этих линий, то есть максимально возможных и реально создаваемых тормозных сил, определяет степень использования сцепления шин с дорогой при торможении, эффективность тормозной системы, вторую важнейшую характеристику тормозов.
Если автомобиль тормозит с замедление меньше критического, то есть его тормозные силы находятся в зоне ниже точки пересечения, то первыми блокируются колёса передней оси, если выше – то, задней.
Дополнительные построения на графике эффективности помогают лучше понять изменение соотношения тормозных сил в процессе торможения.
При торможении автомобиля с максимальным замедлением, с учётом (37), можно записать
Если первой блокируется передняя ось автомобиля, то сила на неё становиться равной предельной по сцеплению. Тогда, подставив предыдущее уравнение в зависимость (60), раскрыв предварительно скобки, получаем уравнение соотношения тормозных сил на осях автомобиля в зависимости от коэффициента сцепления, линию равных сцеплений
F b f ( f h g L a − 1 ) + F b r f h g L a + f g M a f = 0. ( 65 ) <\displaystyle F_
\ f<\frac
Пересечение этой линии с прямой реального соотношения тормозных сил означает блокировку колес передней оси при заданном коэффициенте сцепления.
Для случая блокировки колёс задней оси, в результате аналогичных рассуждений, уравнение линий равных сцеплений будет определяться следующим уравнением
F b r ( f h g L a + 1 ) + F b f f h g L a − f g M a r = 0. ( 66 ) <\displaystyle F_
(f<\frac
Ещё одну вспомогательную, линию равных замедлений, можно построить просто проведя прямую под углом 45°, если масштаб на осях одинаковый. Действительно, сумма пары тормозных сил в любой точке на этой линии одна и та же. Следовательно, и замедление автомобиля также будет постоянным.
Таким образом, при торможении автомобиля на дороге с коэффициентом сцепления равным единице, первой в точке A (см. Рисунок 8) заблокируется задняя ось. Тормозная сила на неё станет предельной по сцеплению. При этом замедление автомобиля будет определяться линий равных замедлений, проходящей через эту точку. Его значение можно найти по пересечению этой линии с кривой предельного по сцеплению соотношения тормозных сил.
В ходе дальнейшего торможения, тормозная сила на задней оси будет немного снижаться в соответствии с линией A-B. Это связано с тем, что замедление автомобиля, продолжая расти, разгружает заднюю ось, уменьшая предельную по сцеплению тормозную силу в соответствии с (52). В точке B заблокируется передняя ось и замедление автомобиля достигнет предельной величины.
Критическое замедление [ править ]
При одновременной блокировке передней и задней осей автомобиля, с учетом ранее выведенных формул (40) и (41) для определения тормозных сил, можно записать
Теперь, если тормозные силы выразить через давление, а затем приравнять давление в передних и задних тормозах (44), то можно получить квадратное уравнение, выражающее критический коэффициент сцепления через параметры автомобиля и его тормозной системы
Найденное в результате решения этого уравнения значение сцепления шин с дорогой будет тем единственным, при котором одновременно блокируются колеса обеих осей данного автомобиля. Соответствующее ему критическое замедление рассчитывается по (62).
Реализуемое сцепление [ править ]
Исследовать тормозные силы можно, также, с помощью кривых реализуемого сцепления. Так называется отношение реальной тормозной силы на оси к вертикальной нагрузке на эту ось
Так как предельная по сцеплению тормозная сила на оси зависит от вертикальной нагрузки, реализуемое сцепление, также, показывает, насколько далека реальная тормозная сила от предельной по сцеплению.
Для построения указанных графиков, сначала, при заданном замедлении, находится давление в главном тормозном цилиндре по (46). Затем, в соответствие с уравнениями (40) и (41), с учётом (44), рассчитываются реальные тормозные силы на осях. Вертикальные нагрузки на оси в зависимости от замедления находятся по зависимостям (49) и (50).
Тогда, из уравнения реализуемого сцепления для передней оси (70), можно записать
и, подставив сюда ограничение по относительному замедлению (72), получить величину, минимально необходимой для выполнения требований, тормозной силы спереди при соответствующем коэффициенте сцепления.
Если вспомнить, что речь идёт о торможении с максимальным замедлением, то из уравнения торможения автомобиля, тормозная сила на задней оси найдётся как
Так это ограничение можно показать на графике эффективности тормозной системы (см. Рисунок 8).
