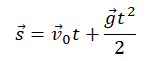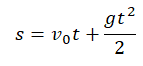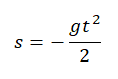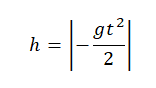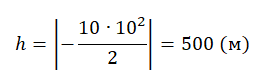с какой скоростью движется второй автомобиль в системе отсчета связанной с первым автомобилем

Содержание

Разбор задач тренировочных заданий по кинематике

В большинстве компьютерных вариантов заданий для каждого участника генерируются свои наборы данных

Задание 1 «С какой скоростью движется вторая машина относительно первой (4 балла)».

Для водителя первой машины скорость второй машины будет складываться из ее скорости относительно земли и скорости земли в системе отсчета первой машины:

Величина относительной скорости второй машины v ₂₁ равна гипотенузе прямоугольного треугольника, образованного скоростями машин относительно земли. По теореме Пифагора находим:

Заметим, если относительная скорость окажется направленной по линии, соединяющей машины, то продолжая двигаться с такими скоростями, они неминуемо столкнутся!

Задание 2 «Вычислите среднюю скорость движения человека (8 баллов)»

Времена t ₁ и t ₂ прохождения первой трети пути и остальных двух третей равны, соответственно

Учитывая, что t = t ₁ + t ₂ находим

Задание 3 «Найдите ускорение и путь автомобиля (8 баллов)»

Находим путь, пройденный на участке разгона:

Скорость при торможении машины меняется по формуле

убывая за время t ₂ до v = 0. Подставляя нуль в правую часть уравнения (1), и выражая величину ускорения, получаем

Соответствующий путь составляет

Задание 4 «Вычислите максимальную высоту подъема тела, брошенного под углом к горизонту (8 баллов)»

Вычислите максимальную высоту подъема тела, брошенного под углом 30 SYMBOL 176 \f «Symbol» к горизонту со скоростью 2 0 м/с. Сопротивлением воздуха пренебрегите.

SYMBOL 97 \f «Symbol» = 30 SYMBOL 176 \f «Symbol»

Используя численные данные, находим:

Задание 5 «Модель: Измерьте скорость тележки (8 баллов)»

Задание: Измерьте с помощью оптических датчиков скорость тележки. Занесите результаты в отчёт (меню в верхней части программы) и отошлите отчёт на сервер.
Стойки с датчиками расположите так, чтобы они фиксировали моменты прохождения тележки. Позицию датчиков можно менять мышью или с помощью пункта ввода.
Конечный результат округляйте до сотых. Пример округления: 0,605 можно округлять до 0,60 или до 0,61.

Рис.1 Начальное состояние системы

Для измерения скорости следует установить стойки с датчиками, например, на позиции с координатами x ₁ =0.2 м и x ₂ =0.8 м и нажать кнопку “Пуск”. Тележка доедет до противоположной стенки и остановится, а на датчиках появятся показания (рис.2).

Рис.2 Конечное состояние системы

Скорость находим как отношение пути между x ₂ и x ₁ к затраченному времени t 2- t 1:

v =( x 2- x 1) /( t 2- t 1)

При этом пусть мы сначала ошибемся и напишем v = (0.8-0.2)/(2.5-0.278) м/с = 0.6/2.222 м/с = 0.270027 … м/ с

(вместо x 2=0.9 м написали x 2=0.8 м). Округляем до сотых: v =0.27 м/ с

Открываем пункт меню “Отчёт…” в верхней части программы, и в появившемся окне вводим это значение (рис.3):

Рис. 3 Отсылка отчёта

Нажимаем кнопку “Отправить результаты на сервер” и получаем отзыв с сервера с информацией о неправильном решении:

Рис.4 Результат проверки со стороны сервера

При нажатии кнопки “Закрыть” любая информация в окне отчета сохраняется и показывается вновь при открытии отчета. При нажатии кнопки “Очистить” восстанавливается первоначальное состояние окна отчета с пустыми пунктами ввода.

Мы можем нажать кнопку “Очистить”, затем кнопку “Закрыть”, проверить правильность наших действий и вычислений.

Например, заново проделать измерения при тех же или других расстояниях между датчиками. Обнаруживаем ошибку и исправляем ее :

v =( x 2- x 1) /( t 2- t 1) = (0.9-0.2)/(2.5-0.278) м/с = 0.7/2.222 м/с = 0.360036 … м/с

Открываем отчет, вводим ответ, отсылаем отчет на сервер и получаем:

Рис.5 Результат проверки нового результата

Итоговый балл за выполнение задания получился 7 из 8 возможных, так как имелась одна дополнительная попытка отсылки результатов на сервер.

Задание 6 «Тест: Кинематика (16 вопросов, 25 баллов)»

Тест будет разбираться в отдельном документе.

Задание 7 «Модель: Измерьте среднюю и мгновенную скорость тележки (12 баллов)»

Задание: По наклонному рельсу из точки с координатой х=0 из состояния покоя начинает равноускоренно двигаться тележка. Определите время движения тележки до её удара о стенку, а также её среднюю и конечную скорость на отрезке от x=0 до x=0.5

Время определите с точностью до тысячных, а остальные величины до сотых, и отошлите результаты на сервер. В промежуточных вычислениях сохраняйте не менее 4 значащих цифр.

Оптические датчики срабатывают при пересечении светового луча датчика флажком тележки. Положение ворот с оптическими датчиками можно изменять при помощи мыши или задавая значения их координат х 1 и х2 при помощи клавиатуры.

На рис.6 показано начальное состояние системы.

Рис.6 Начальное состояние системы

Рис.7 Конечное состояние системы

Полное время движения равно t 2. Средняя скорость v _ср движения на отрезке от x =0 м до x =0.5 м равна x 1/ t 1. Конечная скорость v 1 движения на этом отрезке в два раза больше, так как при равноускоренном движении v _ср = ( v 0+ v 1)/2, а v 0=0. То есть v 1 проще вычислить чем измерить с достаточной точностью.

Источник

С какой скоростью движется второй автомобиль в системе отсчета связанной с первым автомобилем

Автомобиль массой 2 т проезжает верхнюю точку выпуклого моста, двигаясь с постоянной по модулю скоростью 36 км/ч. Радиус кривизны моста равен 40 м. Из приведённого ниже списка выберите все правильные утверждения, характеризующих движение автомобиля по мосту.

1) Равнодействующая сил, действующих на автомобиль в верхней точке моста, сонаправлена с его скоростью.

2) Сила, с которой мост действует на автомобиль в верхней точке моста, меньше 20 000 Н и направлена вертикально вниз.

3) В верхней точке моста автомобиль действует на мост с силой, равной 15 000 Н.

5) Ускорение автомобиля в верхней точке моста направлено противоположно его скорости.

Переведем скорость

Рассмотрим рисунок, поясняющий движение автомобиля по выпуклому мосту.

1. Неверно. Равнодействующая сил реакции опоры N и силы тяжести mg по второму закону Ньютона сонаправлена с вектором ускорения. А т. к. автомобиль движется по окружности, то ускорение направлено к центру окружности, т. е. вниз. Следовательно, и равнодействующая направлена вниз. Скорость автомобиля при движении по окружности направлена по касательной (в данном случае — горизонтально).

2. Неверно. Сила, с которой мост действует на автомобиль — сила реакции опоры — направлена вертикально вверх.

3. Верно. Сила, с которой автомобиль действует на мост, равна весу тела. По третьему закону Ньютона P = N. Найдём силу реакции опоры по второму закону Ньютона Центростремительное ускорение равно Значит, Р = 15 кН.

4. Верно. (см. пункт 3).

5. Неверно. Вектор ускорения направлен вертикально вниз, вектор скорости — горизонтально (см. пункт 1).

Источник

Тест №1 ЕГЭ по физике

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость автомобиля относительно земли ( v ₁), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v ₂). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:

Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:

По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50

Алгоритм решения

Решение

Записываем данные относительно Земли:

Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость второго автомобиля относительно оси ОХ ( v ₂), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v ₁).

Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:

Алгоритм решения

Решение

Записываем исходные данные:

Записываем формулу ускорения:

Так как начальная скорость равна 0, эта формула принимает вид:

Отсюда скорость равна:

Подставляем имеющиеся данные и вычисляем:

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁ и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁ и s₂, а затем сложим их:

На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v₂ больше скорости первого тела v₁ в n раз, где n равно…

Алгоритм решения

Решение

Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:

Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

Алгоритм решения

Решение

Запишем исходные данные:

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

Алгоритм решения

Решение

Записываем исходные данные:

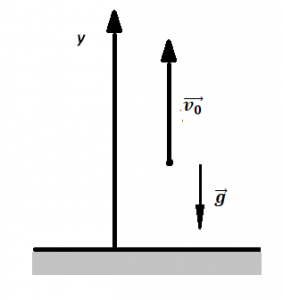
Записываем формулу для определения скорости тела в векторном виде:

Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:

Подставим известные данные и вычислим скорость:

Алгоритм решения

Решение

Записываем исходные данные:

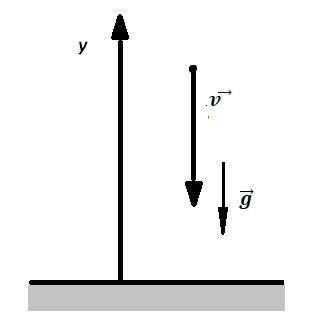
Перемещение (высота) свободно падающего тела, определяется по формуле:

В скалярном виде эта формула примет вид:

Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:

Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:

Вычисляем высоту, подставив известные данные:

Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).

Горизонтальная составляющая скорости шарика определяется формулой:

Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).

Ответом будет следующая последовательность цифр — 33.

Алгоритм решения

Решение

Записываем исходные данные:

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

Источник

С какой скоростью движется второй автомобиль в системе отсчета связанной с первым автомобилем

Два автомобиля движутся в одном и том же направлении со скоростями и относительно поверхности Земли. Скорость света c от фар первого автомобиля в системе отсчета, связанной с другим автомобилем, равна

Согласно второму постулату специальной теории относительности, скорость света одинакова для всех инерциальных систем отсчета. Таким образом, скорость света от фар первого автомобиля в системе отсчета, связанной с другим автомобилем, равна c.

Представим: человек сидит на заднем сидении автобуса, автобус движется со скоростью 100 км/ч, человек начинает двигаться в направление кабины со скоростью 5 км/ч, тогда скорость человека относительно земли будет 105 км/ч.

Представим другую ситуацию: автобус движется со скоростью света, человек встает и начинает двигатся со скоростью 5 км/ч. Тогда получается, что скорость человека относительно земли будет- скорость света+ 5 км/ч.

Автобус не может двигаться со скоростью света. Вы просто не сможете его так разогнать. Это раз.

А во-вторых, привычный нам закон сложения скоростей перестает работать в этой области. Если Ваш гипотетический автобус движется со скоростью всего лишь на один километр в час меньше скорости света, а человек начинает двигаться по нему со скоростью 5 км/ч, то для наблюдателя на земле его скорость все равно будет меньше скорости света.

Правильная формула для закона сложения скоростей в релятивистском случае имеет вид:

Отсюда, кстати следует, что если , то и . То есть если пустить луч света в Вашем автобусе, то и наблюдателю в автобусе, и наблюдателю на земле будет казаться, что свет распространяется со скоростью

Источник

Задание №1 ЕГЭ по физике

В задании №1 ЕГЭ по физике необходимо решить простую задачу по кинематике. Это может быть нахождение пути, скорости, ускорения тела или объекта по графику из условия.

Записываем закон сложения скоростей в векторном виде:

Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:

По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем данные относительно Земли:

Записываем закон сложения скоростей в векторном виде:

Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем исходные данные:

Записываем формулу ускорения:

Так как начальная скорость равна 0, эта формула принимает вид:

Отсюда скорость равна:

Подставляем имеющиеся данные и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁ и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁ и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:

Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем исходные данные:

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем исходные данные:

Записываем формулу для определения скорости тела в векторном виде:

Подставим известные данные и вычислим скорость:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем исходные данные:

Перемещение (высота) свободно падающего тела, определяется по формуле:

В скалярном виде эта формула примет вид:

Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:

Вычисляем высоту, подставив известные данные:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Горизонтальная составляющая скорости шарика определяется формулой:

Ответом будет следующая последовательность цифр — 33.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем исходные данные:

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник